Нелинейная фильтрация сигналов: Учебное пособие, страница 9

Здесь необходимо пояснить, что под термином "нормальные" измерения понимают не только измерения, для которых закон распределения является нормальным (гауссовым). В общем случае p_осн(x) – это закон распределения оценок в ситуациях, когда аномальные измерения отсутствуют (P₀ = 0), и это может быть, например, релеевский, пуассоновский или равномерный закон.

         Соответственно под терминами ²грубая погрешность², ²аномальное измерение² и ²выброс² понимают такой результат измерения или оценку параметра, которая существенно отличается от истинного значения, а также от большинства других оценок в выборке X₁, X₂,…, X_Ns. Термин ²существенно² в этой ситуации нуждается в пояснении или более строгом определении. Ведь если, например, р_осн(х) – гауссов закон распределения с математическим ожиданием (МО) m_x и дисперсией , то по определению р_осн(х)¹0 для хÎ[-¥; +¥] и, следовательно, область определения р_осн(х) пересекается с областью определения р_загр(х), каким бы ни было р_загр(х).

         Поэтому абсолютно корректное разделение оценок на ²нормальное² измерение и ²грубую погрешность² возможно лишь тогда, когда ПРВ р_осн(х) определена  на некотором интервале xÎ[a, b], а р_загр(х) = 0 при  xÎ[a, b]. В остальных же случаях деление оценок на «нормальные» и «аномальные» весьма условно. В частности, для рассмотренного выше примера гауссовой ПРВ р_осн(х) «аномальными» могут считаться такие оценки X_i, для которых >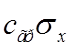, где .

При моделировании выборок, содержащих выбросы, используют различные ПРВ р_загр(х), например:

1) р_загр(х) – гауссова с СКО s_загр>>s_х и математическим ожиданием, которое может быть как равным, так и не равным m_x [12] ;

2) р_загр(х)=1/(b-a), где xÎ[a; b] и выполняется условие (b-a)>>s_x;

3)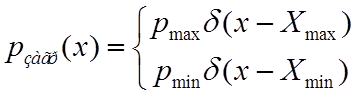, где p_max+p_min=1, d(.) – дельта-функция, X_max и X_min – фиксированные значения, существенно отличающиеся от истинного значения измеряемой величины; при этом X_min меньше (отрицательный выброс), а X_max соответственно больше  (положительный выброс) истинного значения;  такие модели р_загр(х) используются при  анализе эффективности методов обработки изображений [2, 3].

Таким образом, р(х) (10) может быть как симметричной, так и несимметричной относительно математического ожидания распределения р_осн(х). Однако в любом случае при Р_о¹0 возможное наличие  в выборке X₁, X₂,…, X_Ns элементов, принадлежащих р_загр(х), приводит к  снижению точности  оценок параметров ПРВ р_осн(х) (отметим, что в конкретных выборках X₁, X₂,…, X_Ns может быть различное число «грубых погрешностей» при некотором Р_о, задаваемом для генеральной совокупности).

         Снижение точности оценок при использовании заданного метода или алгоритма обработки выборки может проявляться:

1)  в появлении смещенности оценки параметров ПРВ р_осн(х) или увеличении смещенности для случая Р_о¹0 по сравнению со случаем Р_о = 0;

2)  в увеличении дисперсии оценок параметров р_осн(х) и т.д.

Мотивируя целесообразность применения устойчивых методов оценивания, П. Хьюбер в своей книге [12] приводит конкретный пример, когда присутствие в выборке малого числа аномальных измерений (Р_о порядка сотых или тысячных) резко ухудшает характеристики точности оценок. Отметим также, что если относительно плотности р_осн(х) (вида распределения, примерного диапазона возможного изменения МО и дисперсии этого распределения) на практике еще можно сделать какие-то априорные,  основанные на каких-то теоретических или эмпирических данных, предположения и допущения, то относительно вида и характеристик р_загр(х) сделать это обычно сложнее. В связи с этими особенностями формируются общие требования к процедуре устойчивого (робастного) оценивания, суть которых состоит в следующем [12]:

1. Для выбранной модели процедура должна иметь достаточно хорошую (оптимальную или почти оптимальную) эффективность.

2. Процедура обязана быть робастной (устойчивой), иначе говоря, малые  отклонения от предположений о модели должны ухудшать качество процедуры лишь в малой степени, а несколько большие отклонения от допущений модели  не должны приводить к катастрофическим  последствиям.