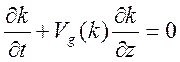Описание электромагнитных волн. Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность электромагнитной энергии. Поток энергии. Уравнения Максвелла для комплексных амплитуд, страница 7

                                                .                                         (10.18)

Неожиданным является то, что при решении линейной задачи получилось нелинейное уравнение для локального волнового числа. Уравнение (10.18) можно привести к характеристической форме (представить в виде обыкновенного дифференциального уравнения в новой системе координат). Существуют несколько процедур для реализации этого. Однако, уравнение (10.18) очень простое и переход к характеристической форме делается, если учесть определение полной (материальной) производной по времени: 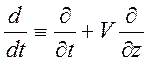, где 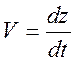 - скорость перемещения точки наблюдения. Значит, характеристическая форма (10.18) имеет вид

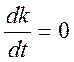                                                            .                                               (10.19)

Это уравнение справедливо на лини

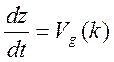                                                            .                                        (10.20)

Линия (10.20) называется характеристикой. На характеристике согласно (10.19)

                                                            ,

а из уравнения характеристики (10.20) следует, что характеристика – прямая линия, так как

                                                            .

Таким образом, возможно следующее определение групповой скорости: это такая скорость перемещения наблюдателя, что он в квазимонохроматической волне видит локальное волновое число постоянным  (локальная частота при этом так же будет константой ).

7). Найдем теперь связь групповой скорости со скоростью переноса энергии плоской монохроматической волной в однородной изотропной среде с временной и пространственной дисперсиями, но без потерь. Для плоской монохроматической волны уравнения Максвелла записываются в виде

                                                ,                                                (10.21)

                                                .                                              (10.22)

Здесь  - вещественная функция.

Перейдем от этих уравнений к уравнениям для приращений  Дифференциалы (10.21) и (10.22) дают

                                                ,               

                                                .

Эквивалентная форма этих соотношений

,                (10.23) .            (10.24)

Умножим (10.23) скалярно на , а уравнение (10.24) – на . Учитывая формулу

                                    ,

Получим

                                    ,            (10.25)

                                    .            (10.26)

Вычитая (10.26) из (10.25), будем иметь

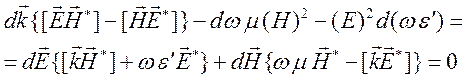                  (10.27)

Равенство нулю правой части это следствие уравнений (10.21), (10.22) при вещественных  и  в среде без потерь. Преобразуем уравнение (10.27), приняв во внимание соотношения

                                   

                                   

                                   

                                    ,

                                    .

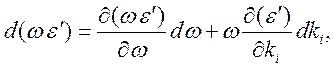
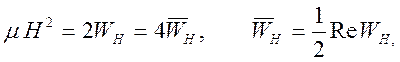
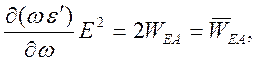
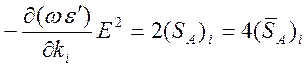Получим (10.27) в виде

                                    .

Здесь  - средняя за период плотность энергии магнитного поля,  - средняя за период плотность электрической и кинетической энергии заряженных частиц вещества,  - составляющая вдоль  средней за период плотности потока кинетической энергии,  - средняя за период плотность потока электромагнитной энергии. Так как для групповой скорости имеем определение

                                                ,

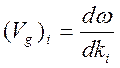то приходим к представлению

                        ,         .

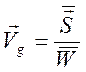В среде без потерь средняя за период энергия сохраняется, уравнение неразрывности имеет вид

                                               

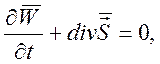
и имеет место связь 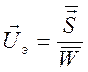 - скорость переноса энергии. Значит,

                                                .

Таким образом, групповая скорость плоской монохроматической волны в среде без потерь совпадает со скоростью переноса энергии этой волной.