![]()
При рассмотрении энергетических соотношений приходится сталкиваться с произведением векторов поля. При этом следует иметь в виду, что
![]()
Для гармонических полей часто важны не сами квадратичные величины, а средние за период значения этих величин. Для таких средних за период квадратичных величин можно получить удобные для использования формулы, дающие представления через комплексные амплитуды.
Определим
мощность, выделяемую на сопротивлении ![]() при
протекании по нему гармонического тока. Ток и напряжение сдвинуты по фазе на
угол
при
протекании по нему гармонического тока. Ток и напряжение сдвинуты по фазе на
угол ![]()
![]() ,
, ![]()
![]()
Здесь
![]() и
и ![]() - это
вещественные функции. Мгновенная мощность определяется соотношением
- это
вещественные функции. Мгновенная мощность определяется соотношением ![]() а средняя за период
а средняя за период ![]() мощность, выделенная на сопротивлении
дается формулой
мощность, выделенная на сопротивлении
дается формулой
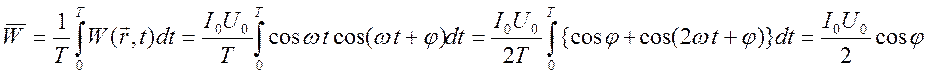 где учтено, что
где учтено, что 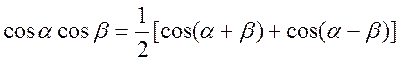 .
.
Этот
же результат можно получить при помощи формального приема. Запишем ![]() и
и ![]() в виде
в виде
![]() ,
, ![]() .
.
Не трудно показать, что
![]()
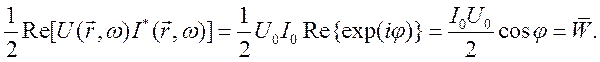
Здесь
значком ![]() обозначена операция комплексного
сопряжения
обозначена операция комплексного
сопряжения
![]() .
.
Так
как вектор Умова – Пойнтинга имеет вид ![]() , то для
гармонических полей среднее за период значение его выражается формулой
, то для
гармонических полей среднее за период значение его выражается формулой
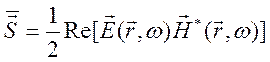 .
.
Исходя из уравнений Максвелла
![]() , (10.6)
, (10.6)
![]() , (10.7)
, (10.7)
получим
энергетическое соотношение, в которое входило бы значение ![]() . С этой целью, считая среду изотропной,
выделим вещественные и мнимые части параметров:
. С этой целью, считая среду изотропной,
выделим вещественные и мнимые части параметров:![]() ,
, ![]() , и перепишем (10.7) в виде
, и перепишем (10.7) в виде
![]() . (10.8)
. (10.8)
Умножая
скалярно уравнение (10.6) на ![]() , а уравнение (10.8) на
, а уравнение (10.8) на ![]() и вычитая одно из другого, получим
и вычитая одно из другого, получим
![]() .
.
Учитывая,
что в левой части этого уравнения стоит ![]() ,
проинтегрируем уравнение по объему
,
проинтегрируем уравнение по объему ![]() , после этого по теореме
Гаусса – Остроградского перейдем от объемного интеграла
, после этого по теореме
Гаусса – Остроградского перейдем от объемного интеграла 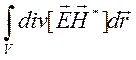 к
интегралу по поверхности
к
интегралу по поверхности ![]() , охватывающей объем
, охватывающей объем ![]() . В результате получим комплексное
энергетическое соотношение для гармонических полей
. В результате получим комплексное
энергетическое соотношение для гармонических полей
![]()
![]()
![]()
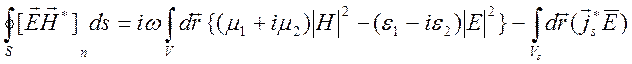 .
.
После
применения операции 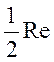 , получим
, получим
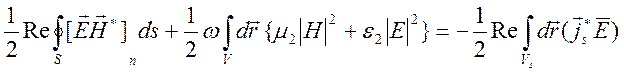 . (10.9)
. (10.9)
Первое
слагаемое здесь представляет средний за период поток энергии через площадь ![]() . Если
. Если ![]() , то
энергия уходит из объема
, то
энергия уходит из объема ![]() . Второе слагаемое при
. Второе слагаемое при
![]() соответствует магнитным и электрическим
потерям энергии внутри объема на нагревание среды. В принципе, возможны случаи
неравновесных (активных сред), в которых
соответствует магнитным и электрическим
потерям энергии внутри объема на нагревание среды. В принципе, возможны случаи
неравновесных (активных сред), в которых ![]() .
Правая часть (10.9) - это работа сторонних сил за период на нагревание среды и
на излучение электромагнитной энергии.
.
Правая часть (10.9) - это работа сторонних сил за период на нагревание среды и
на излучение электромагнитной энергии.
Рассмотрим
связь между векторами ![]() и между векторами
и между векторами ![]() . Представим
. Представим ![]() ,
, 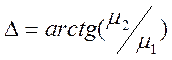 ,
, 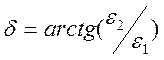 .
.
При ![]() ,
, ![]() имеем
имеем ![]() . С
учетом представлений для комплексных амплитуд
. С
учетом представлений для комплексных амплитуд
![]() ,
,
![]()
получается связь между гармоническими полями
![]() ,
,
![]() .
.
Уравнениям
![]()
![]()
соответствует эллипс (Рис 10.1)
на плоскости ![]() . За один период точка на этой плоскости
пробегает по эллипсу. Потери энергии пропорциональны площади этого эллипса. В
случае
. За один период точка на этой плоскости
пробегает по эллипсу. Потери энергии пропорциональны площади этого эллипса. В
случае ![]() векторы
векторы ![]() и
и ![]() эллипс вырождается в прямую линию,
магнитные потери отсутствуют. Аналогичными свойствами обладают векторы
эллипс вырождается в прямую линию,
магнитные потери отсутствуют. Аналогичными свойствами обладают векторы ![]() и
и![]() .
.
10.5. Энергия поля в
диспергирующих средах. Для изменения электрической и магнитной индукций ![]() и
и ![]() на
величину
на
величину ![]() и
и ![]() в
единичном объеме необходимо затратить работу
в
единичном объеме необходимо затратить работу
![]() .
.
В случае
статических полей и в случае сред без дисперсии индукция ![]() зависит только от поля
зависит только от поля ![]() и через диэлектрическую проницаемость от
температуры среды. В особом типе кристаллов (сегнетомагнетики) ситуация
сложнее:
и через диэлектрическую проницаемость от
температуры среды. В особом типе кристаллов (сегнетомагнетики) ситуация
сложнее: ![]() зависит от трех полей
зависит от трех полей ![]() . Аналогичными свойствами обладает и поле
. Аналогичными свойствами обладает и поле ![]() . Поэтому, при постоянной температуре
. Поэтому, при постоянной температуре ![]() является полным дифференциалом
термодинамической функции
является полным дифференциалом
термодинамической функции ![]() (она называется
плотностью свободной энергией)
(она называется
плотностью свободной энергией)
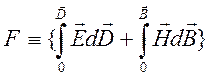 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.