Описание электромагнитных волн. Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность электромагнитной энергии. Поток энергии. Уравнения Максвелла для комплексных амплитуд, страница 2

                                                .

Здесь  и  - это вещественные функции. В принципе, вместо знака «-» перед  можно брать знак «+», переход от одного случая к другому осуществляется операцией комплексного сопряжения. Введем обозначение для комплексной амплитуды  и придем к представлению

                                                ,

функция  - это Фурье-образ функции . В соответствии с этой формулой каждый входящий в (10.1) – (10.5) вектор и скалярную функцию можно записать в таком же виде. Например,

                                               

С учетом такого представления для гармонических полей и того, что , уравнение (10.1) записывается в виде

                                    .

Поскольку это уравнение должно выполняться в любой момент времени, то приходим к уравнению для комплексных амплитуд

.

Аналогично записываются и другие уравнения:

                                    ,

                                    ,

                                    .

В среде без пространственной дисперсии, в линейной электродинамике материальные уравнения для комплексных амплитуд имеют вид

                                    ,

                                    .

С учетом этих материальных соотношений, уравнения Максвелла принимают вид

                                    ,

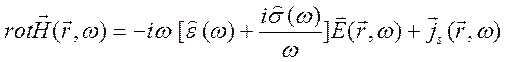или

                                    ,

где введено обозначение

                                    ,

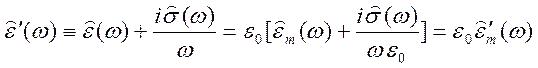где  - тензор комплексной проницаемости среды,  - тензор относительной комплексной проницаемости среды. В случае изотропной среды , где  - единичный тензор.

Уравнение неразрывности приводится к виду

                                                .

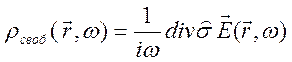Система уравнений Максвелла для комплексных амплитуд в случае линейной электродинамики при отсутствии пространственной дисперсии имеет вид

                                                ,

                                                ,

                                                ,

                                                ,

где имеет место материальное соотношение

.

10.3. Диэлектрическая проницаемость при очень больших частотах. В пределе  функция . Это очевидно из простых физических соображений: При достаточно быстром изменении поля, процессы поляризации, приводящие к установлению отличной от  индукции , вообще не успевают происходить. Можно установить предельный вид функции  для любых сред при больших частотах. Частота поля должна быть велика по сравнению с частотами движения всех электронов в атомах данного вещества. Электроны в такой ситуации можно считать свободными, пренебрегая их взаимодействием друг с другом и с ядрами атомов.

            Скорость движения  электронов мала по сравнению со скоростью света . Поэтому расстояние  , проходимое электроном в течении периода волны, малы по сравнению с длиной волны . Поле волны можно считать однородным и уравнение движения, описывающее возмущение скорости взять в виде

                                    .

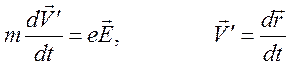Отсюда получаем связь между комплексными амплитудами

                                          

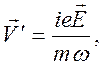
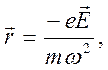
Вектор поляризации  - это дипольный момент единицы объема

                                   

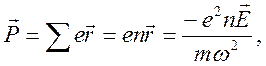
где  - концентрация электронов (во всех атомах единичного объема). Так как справедливо

                                    ,

то имеем

                                    .

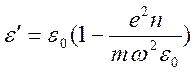Фактическая область применимости этой формулы начинается от далекого ультрафиолета у самых легких элементов или от рентгеновских частот у более тяжелых элементов. Величина 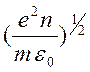 имеет размерность частоты, она называется плазменной частотой. При  происходит предельный переход .

В окрестности переднего фронта волны имеется резкое изменение поля, которое описывается высокими частотами. Значит, фронт распространяется в среде с диэлектрической проницаемостью вакуума. Скорость распространения переднего фронта равна скорости распространения света

10.4. . Энергетические соотношения для стационарных процессов. Под стационарными процессами, будем здесь понимать процессы, гармонически зависящие от времени. Для них задача сводится к решению уравнений Максвелла для комплексных амплитуд. После их нахождения, переход к реальным полям осуществляется по формуле