Описание электромагнитных волн. Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность электромагнитной энергии. Поток энергии. Уравнения Максвелла для комплексных амплитуд, страница 4

В простейшем случае линейных полей в среде без дисперсии  свободная энергия имеет вид

                                                          ,

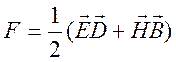в изотропной среде происходит дополнительное упрощение

                                                          .

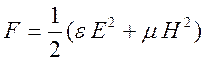В  входит не только энергия самого поля, но и свободная энергия вещества, связанная с полем.

              Если  - плотность энергии и плотность энтропии, то имеет место термодинамическое соотношение

                                                          ,

где  - температура, . Если  и  не зависят от температуры, то .

              В случае переменных во времени полей и при наличии дисперсии ситуация усложняется. При этом величина  не представляет собой полный дифференциал, хотя сохраняет смысл работы по изменению индукциий  и  (работа, совершаемая над системой). Согласно первому началу термодинамики

                                                          ,

где  - изменение внутренней энергии,  - изменение теплоты, выделяемой в единичном объеме вещества. Следует подчеркнуть, что  не является полным дифференциалом, какой либо функции. Знание  не позволяет определить обе величины  и  порознь, так как нужно знать еще динамику вещества (это определяет энергию вещества в поле).

10.6. Фазовая и групповая скорости. Различные способы введения понятия групповой скорости. Скорость переноса энергии.

        1). Понятие фазовой скорости относится к плоской монохроматической волне . Рассмотрим закономерность перемещения поверхности равной фазы .

,

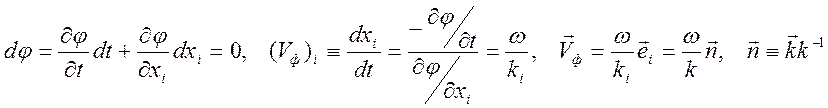где  - фазовая скорость данной плоской монохроматической волны. Так как для конкретной среды  и  связаны дисперсионным  соотношением, то фазовая скорость является функцией частоты и волнового вектора, в общем случае эта функция может быть комплексной. Произвольное поле  может быть представлено как суперпозиция плоских монохроматических волн.

            Рассмотрим процесс в среде с временной дисперсией. Для простоты ограничимся случаем  и воспользуемся представлением

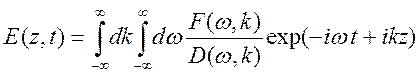                                    .                         (10.9)

Где  - дисперсионное алгебраическое уравнение для данной сплошной однордной среды. Это уравнение может иметь несколько корней, соответствующих различным типам волн и различным направлениям их распространения. Рассмотрим только одну волну, описываемую корнем дисперсионного уравнения . Первое интегрирование (10.9) по вычету можно проводить либо по , либо по . Сделаем первое интегрирование по  и для одного типа волны получим

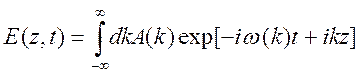                                    .                                   (10.10)

Выясним смысл функции , для этого рассмотрим (10.10) в момент времени

                                    .

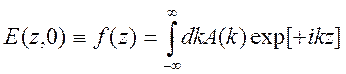Согласно теореме Фурье этот интеграл можно обратить и найти

                                    .

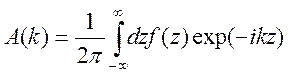Эта формула определяет фурье – образ функции .

            2). Сначала рассмотрим простейший случай, когда отсутствует дисперсия (при этом 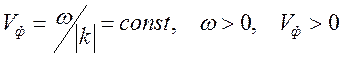). Рассмотрение случая отсутствия дисперсии позволить выяснить простейшие идеализированные закономерности. В этом случае возможно представление (10.10) в виде

                        .

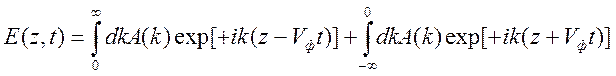Здесь учтено, что при  имеет место .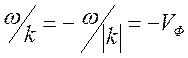

Первое слагаемое представляет собой некоторую функцию, зависящую от А второе – функцию от :

                                    ,    .

Первое слагаемое описывает волну, распространяющуюся вдоль положительного направления оси , а второе – волну, бегущую в противоположном направлении. Обе эти волны не меняют формы в процессе своего распространения со скоростью  в среде без дисперсии. Конечно, этот результат может быть получен и не прибегая к преобразованию Фурье – это следует непосредственно из волнового уравнения для поля .

            3). В реальной ситуации идеализация среды без дисперсии нарушается. Как уже отмечалось выше, в любом веществе в пределе  диэлектрическая проницаемость стремится к проницаемости вакуума. Уже этот факт указывает на наличие временной дисперсии. Существование дисперсии это следствие общих физических принципов. Рассмотрим среду с дисперсией, но сначала ограничимся простейшим случаем суперпозиции только двух плоских монохроматических волн с близкими частотами и волновыми векторами и одинаковыми амплитудами: