Нелинейные и параметрические цепи, страница 6

Можно получить чистое преобразование на разностную частоту без нелинейных элементов? Можно. Для этого надо иметь перемножающие устройства. Их реализуют, как параметрические устройства, без нелинейных элементов. Напишем равенство. . Надо реализовать его правую часть. Блок схема такого устройства приведена на рис. 4.20. Получили чистое преобразование, только разностная частота. Не надо никаких фильтров. Устройство получается сложное, но принципиально возможное.

Такие преобразователи используются при приёме слабых сигналов на фоне помех, шумов, когда присутствие нелинейных элементов очень не желательно.

4.6.5. Модуляция.

При модуляции происходит перенос спектра низкочастотного сигнала на частоту несущей. Рассмотрим процесс получения амплитудно - модулированного сигнала, используя опять простейшую схему. Реальные схемы модуляторов реализуются, как правило, на транзисторах и могут быть очень разнообразными и сложными. Нам сейчас важна принципиальная возможность.

Имеем два сигнала, низкочастотный  и на несущей частоте . Всё очень похоже на предыдущее преобразование, только . Схема изображена на рис. 4.17а. В этом эксперименте положим  и примем апроксимацию ВАХ как на рис. 4.23б. На входе мы имеем сумму сигналов , рис. 4.21. Две спектральные составляющие с частотами  и . Ток в цепи будет протекать, когда . При этом, выходное напряжение,  воспроизведёт верхнюю половину картинки на рис. 4.21. Нижняя половина () будет ограничена диодом. Анализ спектра тока даёт  результат, изображённый на рис. 4.22а. В спектре будут представлены частоты самих сигналов и комбинационные частоты  и др. Амплитудно-модулированный сигнал , рис. 4.22б, получится, если выделить фильтром группу из трёх гармонических составляющих с частотами  и .

Если апроксимировать ВАХ нелинейного сопротивления полиномом, как в предыдущем пункте для задачи преобразования частоты, то мы получим полный набор комбинационных частот, представленных на рис. 4.18б (здесь ). Линейный член даст нам сигнал на несущей частоте. За счёт квадратичного члена (произведения) мы получим нужные нам комбинационные частоты . Однако в этом случае, за счёт кубичного члена, возможно появление комбинационной частоты . Гармонический характер модуляции будет нарушен.

Чистую модуляцию без всяких комбинационных частот можно получить, если просто перемножить сигналы  и , а затем сложить результат с сигналом несущей частоты.

Отметим ещё раз важное значение этой операции. Без модуляции практически невозможна передача информации на большие расстояния без проводов (радиовещание, телевидение, различные средства радиосвязи).

Скажем несколько слов о частотной модуляции. Она получается без нелинейных элементов. Частота колебаний генератора определяется параметрами колебательного контура. Меняя индуктивность или ёмкость, мы можем изменить частоту генератора и получить сигнал модулированный по частоте. Это типичный параметрический эффект.

4.6.6. Детектирование.

Это процесс обратный по отношению к модуляции, процесс восстановления низкочастотного сигнала из узкополосного модулированного. Всё очень похоже на выпрямление. Имеем на входе амплитудно-модулированный сигнал  (), рис 4.22б. Хотим получить низкочастотный сигнал .

Используем опять простейшую схему и апроксимацию ВАХ нелинейного сопротивления цепи для больших сигналов, рис. 4.23а,б. Цепь фильтра пока не учитываем. Ток в цепи будет протекать только при , рис. 4.23в. , где  есть крутизна ВАХ. Если бы модуляции не было (), то получился бы ток , как в схеме ограничителя (однополупериодный выпрямитель без ёмкости), рис. 4.8. Такой сигнал мы уже анализировали. 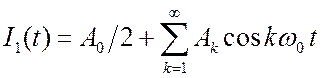; ; . При наличии модуляции мы имеем произведение . В спектре тока появилась низкочастотная составляющая с амплитудой . Выделяя её ФНЧ, мы получим ожидаемый сигнал . Остальные спектральные составляющие нас не интересуют. Поскольку , то реально в качестве ФНЧ используется часто просто интегрирующая цепочка, как на рис. 4.23а.