Нелинейные и параметрические цепи, страница 2

2. Необходимость использования разных сопротивлений для постоянных и переменных составляющих токов и напряжений. Обратимся к рис. 4.7а. Сопротивление диода для постоянных составляющих определяется следующим образом. . Обозначается оно по-разному: . Чем меньше , тем больше угол . Дифференциальное сопротивление (для приращений), или сопротивление для переменных составляющих, . В пределе, оно определяется как производная, . Часто удобнее использовать проводимость  или «крутизну» характеристики. Чем круче идёт ВАХ, тем меньше . Для изображённой ВАХ . Для реальных пассивных элементов  всегда, в то время как  может быть и отрицательным. Примеры таких нелинейных элементов мы рассмотрим позже.

Для линейных элементов ВАХ есть прямая линия и . Нет смысла вводить два сопротивления.

В каких ситуациях реализуется дифференциальное сопротивление? Когда мы имеем малые изменения напряжения и тока относительно средних значений. Например, в изображённой на рис. 4.7б схеме, для источника переменного напряжения  будет реализовано дифференциальное сопротивление диода. Для источника постоянного напряжения  будет реализовано .

3. Преобразование спектра сигнала нелинейными элементами. Проиллюстрируем эту особенность нелинейной цепи на конкретном примере диодного ограничителя, рис 4.6а. Для упрощения рассуждений примем ВАХ нелинейного сопротивления цепи (с учётом R) такой, как изображено на рис. 4.8а. Это типичное представление характеристики для больших сигналов. Постоянное сопротивление , где  есть прямое сопротивление диода, когда ток течёт в прямом направлении и бесконечное, для обратного направления. Пусть  и . Тогда положительные полупериоды входного сигнала будут передаваться на выход, практически без изменения, а отрицательных не будет (тока нет). Они будут полностью ограничены. Форма тока в цепи представлена на рис. 4.8б. Спектр такого сигнала мы уже анализировали, формула (2.10).

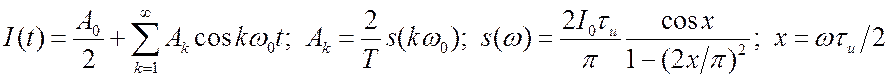. Для этого примера: . Тогда:  есть постоянная составляющая; , где  . На входе мы имели гармонический сигнал, а на выходе получили сигнал, в спектре которого появились новые гармонические составляющие, постоянная составляющая и чётные гармоники основной частоты . В этом и состоит очень важная особенность нелинейных элементов, определяющая их широкое применение.

Вспомним особенность линейных цепей. Если на вход линейной цепи подать гармонический сигнал частоты , то все напряжения и токи в этой цепи будут меняться по гармоническому закону с той же частотой (когда закончатся переходные процессы). Для решения задачи надо определить всего два параметра, амплитуду и сдвиг фазы сигнала по отношению ко входному. Никаких новых частот.

Негармонический сигнал в линейной цепи тоже искажается, например, в интегрирующей цепи. На входе скачок напряжения, а на выходе непрерывное изменение. Искажение сигнала произошло потому, что цепь изменила соотношение амплитуд и фаз гармонических составляющих входного сигнала. Такие искажения часто называют «линейными», в отличие от «нелинейных», когда в спектре выходного сигнала появляются новые гармонические составляющие.

4.5.  Методы анализа нелинейных цепей.

Фактически, это те методы, которые используются для решения нелинейных алгебраических и дифференциальных уравнений. Мы остановимся очень кратко на некоторых.

Особенность ситуации состоит ещё в том, что ВАХ (или другая характеристика нелинейного элемента) задаётся нам экспериментально, приближённо (график, таблица). Она индивидуальна. Точный аналитический закон изменения мы не знаем. Поэтому очень важную роль играют приближённые методы решения, и прежде всего, графический, как наиболее простой и доступный. Перечислим некоторые методы.

1. Графический метод. Простой, наглядный. Очень удобен для получения качественных результатов, однако позволяет получить и надёжные количественные результаты. Мы его уже использовали (ограничитель) и ещё будем использовать.