Нелинейные и параметрические цепи, страница 4

. Отсюда: . Вычитая первое равенство из второго, будем иметь: . В итоге: . Обычно 0,5 - 0,7, а . Наличие  ухудшает стабилизацию. Сопротивление  определяется проще всего с помощью графического построения. Надо провести прямую через точку  на оси напряжений и середину рабочего участка ВАХ. Наклон этой нагрузочной прямой и даст нам .

Мы рассмотрели пример простейшего параллельного стабилизатора, в котором нелинейный регулирующий элемент включён параллельно нагрузке. Коэффициент стабилизации таких стабилизаторов получается порядка 20 – 30. Кроме того, они имеют очень маленький коэффициент полезного действия (порядка 15% ). Для сравнения укажем, что у хороших последовательных стабилизаторов  достигают значений сотен и тысяч.

Для стабилизации тока нелинейный элемент должен иметь на ВАХ участок с очень большим дифференциальным сопротивлением. Такой участок имеют транзисторы. При постоянном сопротивлении нагрузки стабилизация тока будет обеспечена, если будет стабилизировано напряжение. Так часто и делают.

4.6.2.  Выпрямление тока. Ограничение.

Во всех преобразователях переменного напряжения в постоянное (источники питания приёмников, телевизоров, приборов и бытовой техники) происходит «выпрямление» тока. Простейшая однополупериодная схема выпрямителя изображена на рис. 4.12а. . Мы уже анализировали её работу без конденсатора (пункт 4.4.,ограничитель). Выпрямление было, но малоэффективное. Сравнительно малая постоянная составляющая напряжения () и очень большие «пульсации» ().

Конденсатор делает работу выпрямителя более эффективной, если его ёмкость выбрана правильно. Должно выполняться сильное неравенство . Тогда конденсатор не успевает заметно разрядиться за период T  и напряжение на нём меняется мало, рис. 4.12б. Пунктиром изображено  (или  без конденсатора). Диод работает как «ключ» (открыт, закрыт). Он открывается только на короткий промежуток , когда . Конденсатор быстро заряжается от источника с малым сопротивлением  почти до амплитудного значения входного напряжения. Потом диод закрывается и конденсатор разряжается медленно через нагрузку. Цепь линейна, . В результате, на выходе мы имеем большую постоянную составляющую, близкую к амплитудному значению  и малые «пульсации», порядка . То, что надо.

На практике широко используется более сложная, двухполупериодная мостовая схема (схема Греца), содержащая 4 диода, рис. 4.13а. Они работают пáрами. Ток в нагрузке течёт в одном направлении, независимо от полярности входного напряжения. Результат изображён на рис. 4.14. Если конденсатора нет, то  изображено пунктиром. При этом, постоянная составляющая равна , амплитуда второй гармоники значительна (), «пульсации» порядка. Поставим конденсатор необходимой ёмкости (). Результаты сразу станут похожи на те, что мы имели для простой схемы. Только период изменения будет в два раза меньше.

Другая типичная реализация двухполупериодной схемы выпрямителя представлена на рис. 4.13б. Здесь всего два диода, но зато нужно удвоенное напряжение источника (фактически два одинаковых источника). Ради упрощения анализа таких схем, иногда реальный нелинейный четырёхполюсник заменяют гипотетическим двухполюсником с чётной ВАХ, как на рис. 4.14. Напомним, что любая ВАХ может быть разложена на чётную и нечётную части. Выпрямление обеспечивается только чётной частью (чётные степени апроксимирующего полинома). Нечётную часть можно не принимать во внимание.

4.6.3.  Умножение частоты.

Пусть мы имеем гармонический сигнал с частотой , а нужен сигнал с частотой . Идея преобразования проста. Если исходный сигнал ограничить (исказить), то появятся гармоники. Нужную гармонику выделяем фильтром. Режим ограничения подбираем таким, чтобы амплитуда нужной гармоники была максимальной. Схема и необходимые построения изображены на рис. 4.15. Пусть , а  постоянно. . ВАХ нелинейного сопротивления  (с учётом R) апроксимируем отрезками прямых, как указано на рисунке. Когда , тока в цепи нет. Когда , , где S  есть крутизна ВАХ (наклон). Получили чётную периодическую функцию с периодом . Пусть  определяет момент отсечки тока или время отсечки, тогда  есть угол отсечки. Запишем явное выражение тока на промежутке . . При , . Отсюда . Угол отсечки изменяется путём изменения . . Разложим теперь  в ряд Фурье. 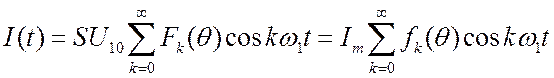. Функции  определяют амплитуды гармоник в зависимости от угла отсечки. Функции Берга  менее удобны на практике, из-за нормировки на . Вычисления дают следующие выражения для функций : ; . Все . , если . Первые две функции не представляют интереса для операции умножения. Они изменяются монотонно от нуля до единицы с ростом угла отсечки. Следующие три функции изображены на рис. 4.16.