Решение задачи Коши для обыкновенных дифференциальных уравнений, страница 7

Вычисляя значения y_i приближенными методами, занесем в таблицу 1 максимальные погрешности каждого метода при различных значениях M (10, 20, 40).

Таблица 1

Поведения максимальной погрешности приближенных методов

    Построим график на отрезке [1,3] функции точного решения (y(x) = 4/x) и вынесем точки (x_i, y_i), соответствующие массивам приближенных решений, полученных по приближенным методам для M = 10:

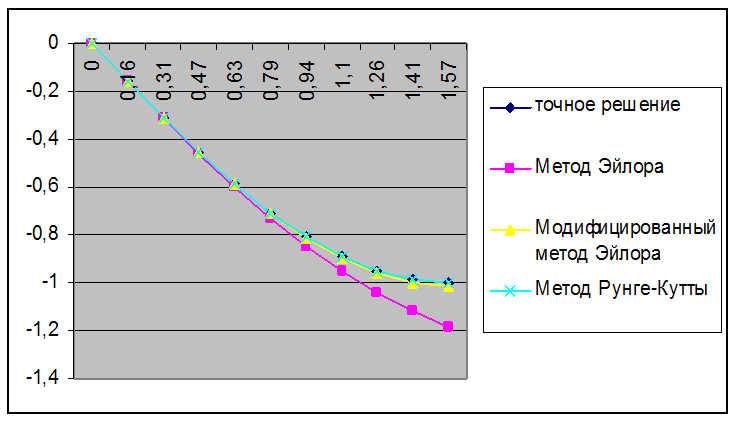
       Вывод: из таблицы 1 видно, что в сравнении с точным решением самым точным является метод Рунге-Кутты; при увеличении M погрешность данного метода уменьшается в 9 раз, что говорит о том, что приближенный метод имеет третий порядок точности. Погрешность модифицированного метода Эйлера (предиктор-корректор) при увеличении M уменьшается в 4 раза, из этого следует, что метод имеет второй порядок точности. Метод Эйлера из перечисленных приближенных методов является менее точным, его погрешность с увеличением M уменьшается в 2 раза, метод имеет первый порядок точности. Сделанные выводы подтверждает и график, который показывает, что ломанные, соответствующие методу Рунге-Кутты (третий порядок аппроксимации) и методу предиктор-корректора (второй порядок аппроксимации), проходят ближе к графику точного решения, чем ломанная, полученная по методу Эйлера первого порядка аппроксимации. Наиболее ближе к графику точного решения проходит ломанная метода Рунге-Кутты, что еще раз свидетельствует об его третьем порядке аппроксимации.