Стійкість нелінійних систем. Методи Ляпунова. Функції Ляпунова. Їхні основні властивості. Теореми Ляпунова, страница 5

Так як, похідна є знакопостійною від’ємною функцією, то з теореми 1 маємо, що нульове розв'язання досліджуваної системи стійке (але не асимптотично).

Приклад 3. Дослідити стійкість системи.

,     .

Розв’язання. Виберемо функцію  у вигляді  й обчислимо .

.

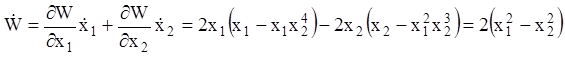Функція W має наступні властивості:

1)   в області ,  на границі цієї області  ;

2)   в області . Тоді з теореми 3 витікає, що нульове розв'язання заданої системи нестійке.

3.11 Встановлення знакоприналежності функцій Ляпунова

З вище розглянутого витікає, що для практичного користування функціями Ляпунова необхідно вміти визначати знак цих функцій й їхніх повних похідних. Яких-небудь загальних правил установлення знакоприналежності цих функцій не існує. Розглянемо деякі положення, що дозволяють у деяких важливих випадках спростити розв'язання такої задачі.

Нехай дана функція Ляпунова , знаковизначена й, що володіє в околиці початку координат неперервними частинними похідними першого порядку. Розкладемо цю функцію в ряд Маклорена:

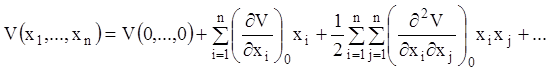                        (3.66)

На підставі (3.58) . Так як знаковизначення функції Ляпунова при  мають екстремум: мінімум – додатньо-визначені й максимум – від’ємне –визначені, то на початку координат повинні виконуватися необхідні умови екстремуму, тобто , .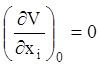

З огляду на сказане, одержуємо

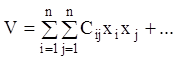                                                           (3.67)

де

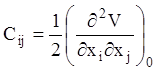 ,                                                     (3.68)

З (3.67) витікає, що розкладання в ряд Маклорена знаковизначеної функції  в ряд по степенях  не містить вільного члена, членів першого степеня відносно , а це значить, що знак функції  в околиці крапки екстремуму  збігається зі знаком відповідної квадратичної форми .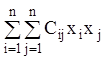

Коефіцієнти  квадратичної форми (3.65) утворять матрицю

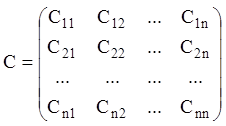                                                         (3.69)

З лінійної алгебри відомо, що для квадратичних форм справедливий наступний критерій Сильвестра: щоб квадратична форма була додатньо-визначеною, необхідно й досить, щоб всі головні діагональні мінори її матриці  були додатні, тобто

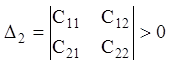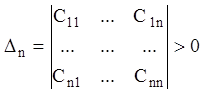, ,…, (3...70)

Таким чином, критерій Сильвестра є достатньою умовою додатної визначеності функції . Якщо функція  обумовлено-від’ємна, то функція (- ) обумовлено-від’ємна. Звідси витікає, що достатньою умовою безперечно заперечності квадратичної форми (3.67) і функції  буде умова (3.70), написана для матриці , що утворюється із матриці  при заміні знаків у всіх її елементів на протилежні. У результаті одержимо умови:

, , , ,…

Таким чином, умова безперечно заперечності квадратичної форми (3.67) і функції  полягає в тому, що мінори  парного порядку повинні бути додатні, а непарного – від’ємні.

Приведемо без доказу ще деякі положення, якими можна скористатися при аналізі конкретних функцій Ляпунова:

1)  розкладання в ряд по степенях , , знаковизначеної функції не може починатися зі членів непарного степеня;

2)  будь-яка однорідна щодо незалежних змінних  функція непарного порядку ,  є функція знакозмінна;

3)  знаковизначеність, як і знакоперемінність, форми  не порушиться, якщо до неї додати будь-яку форму того ж порядку  з досить малими коефіцієнтами.

Приклад 1. Дослідити знак функції в околиці

Розв’язання. Розкладаємо в ряд Маклорена функції

,     .

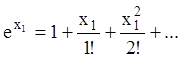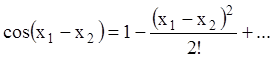Тоді в околиці початку координат одержуємо розкладання функції  в ряд Маклорена:

 .

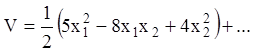Матриця коефіцієнтів квадратичної частини функції  буде 

.

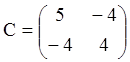Обчислимо головні діагональні мінори

,

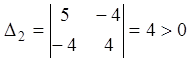
звідси на підставі критерію Сильвестра містимо, що задана функція безперечно додатна.

Приклад 2. Дослідити стійкість збуреного руху

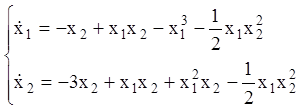
Розв’язання е. Функцію Ляпунова візьмемо у вигляді

.

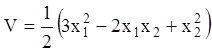Матриця коефіцієнтів квадратичної форми

.

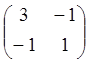звідки , 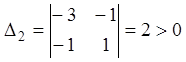. Звідки витікає, що функція  обумовлено-додатна. У силу заданих рівнянь збуреного руху обчислюємо похідну

.

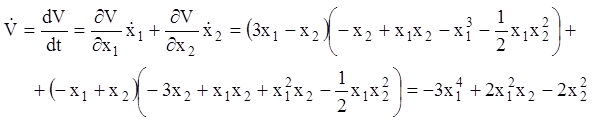Розглядаючи  як квадратичну форму, уважаючи за змінні  й . Матриця коефіцієнтів цієї квадратичної форми

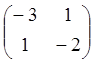
Звідки , .

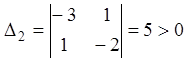Звідси маємо, що похідна   є обумовлено-від’ємною функцією відносно й , а отже, і щодо змінних  й . Тоді по теоремі 2 нульове розв'язання заданої системи асимптотично стійке.