![]() ,
, ![]() .
.
Записуємо характеристичне рівняння й знаходимо характеристичні числа
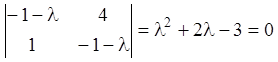
![]()
![]() ,
,
![]() .
.
Тому що одне з характеристичних чисел додатне, то нульове розв'язання заданої системи нестійке.
Приклад 2: Дослідити стійкість збуреного руху
![]() ,
, ![]() .
.
Розв’язання В околиці
точки спокою ![]() справедливі розкладання Маклорена:
справедливі розкладання Маклорена: 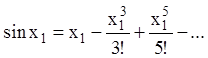 ,
, 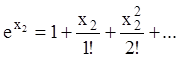 . З
огляду на розкладання, система першого наближення запишеться
. З
огляду на розкладання, система першого наближення запишеться
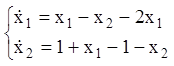 або
або 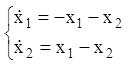 .
.
Записуємо характеристичне рівняння й знаходимо його корені
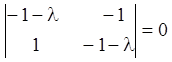 ,
, ![]() ,
,
![]() .
.
Так як, дійсні частини характеристичних чисел від’ємні, то нульове розв'язання нелінійної системи асимптотично стійке.
Приклад 3. Дослідити стійкість нелінійної системи
![]() ,
, ![]() .
.
Розв’язання. Система першого наближення
![]() ,
, ![]()
вирішуємо характеристичне рівняння
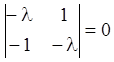 ,
, ![]() ,
, ![]() .
.
Тому що дійсні частини характеристичних чисел дорівнюють нулю, то в цьому випадку по рівняннях першого наближення не можна судити про стійкість нульового розв'язання нелінійної системи.
Розглянемо деякий збурений стаціонарний рух
![]() (3.56)
(3.56)
де функції ![]() неперервні в області
неперервні в області ![]() , де
, де ![]() - деяка
постійна й допускає єдине розв'язання системи (3.56) для будь-яких початкових
умов й у силу стаціонарності руху не залежить явно від
- деяка
постійна й допускає єдине розв'язання системи (3.56) для будь-яких початкових
умов й у силу стаціонарності руху не залежить явно від ![]() .
.
Так як аналітичне розв'язання системи (3.56), як правило, одержати
неможливо, основним методом дослідження стійкості руху системи є другий
(прямій) метод Ляпунова. Відповідно до цього методу введемо в розгляд дійсні
функції ![]() , де
, де ![]() -
варіації, визначені в деякій околиці точки рівноваги
-
варіації, визначені в деякій околиці точки рівноваги
![]() ,
, ![]() (3.57)
(3.57)
однозначні й неперервні разом зі своїми першими частинними похідними в цій околиці й рівноваги, що звертаються в нуль у точці
![]() .
(3.58)
.
(3.58)
Введемо деякі поняття щодо цих функцій.
Означення 1. Функція
![]() називається знаковизначеною (від’ємною
визначеною або додатною – визначеною), якщо вона за умови (3.57) (
називається знаковизначеною (від’ємною
визначеною або додатною – визначеною), якщо вона за умови (3.57) (![]() - досить мале додатне число) може приймати
значення тільки одного визначеного знака й звертається в нуль тільки при
- досить мале додатне число) може приймати
значення тільки одного визначеного знака й звертається в нуль тільки при ![]() .
.
Означення 2.
Функція ![]() називається знакопостійною (додатної або невід’ємної),
якщо вона в області (3.57) може приймати значення тільки одного визначеного
знака, але може звертатися в нуль і при
називається знакопостійною (додатної або невід’ємної),
якщо вона в області (3.57) може приймати значення тільки одного визначеного
знака, але може звертатися в нуль і при ![]() .
.
Означення 3. Функція
![]() називається знакозмінної, якщо вона не є
ні знаковизначеною, ні знакопостійною, і, отже, як би не було мало число
називається знакозмінної, якщо вона не є
ні знаковизначеною, ні знакопостійною, і, отже, як би не було мало число ![]() , і може приймати в області (3.57) як
додатні, так і від’ємні значення.
, і може приймати в області (3.57) як
додатні, так і від’ємні значення.
У теорії стійкості вивчається поведінка функції ![]() уздовж фазових траєкторій
досліджуваної системи диференціальних рівнянь для того, щоб на основі такого
вивчення зробити висновок про стійкість і нестійкість траєкторій. Функції
уздовж фазових траєкторій
досліджуваної системи диференціальних рівнянь для того, щоб на основі такого
вивчення зробити висновок про стійкість і нестійкість траєкторій. Функції ![]() , що мають указане вище призначення,
називають звичайно функціями Ляпунова. Розглянемо найпростіші приклади
таких функцій.
, що мають указане вище призначення,
називають звичайно функціями Ляпунова. Розглянемо найпростіші приклади
таких функцій.
Приклад 1. Розглянемо
функцію ![]() . У будь-якій точці
. У будь-якій точці ![]() відмінної
від початку координат вона приймає тільки додатні значення й звертається в нуль
при
відмінної
від початку координат вона приймає тільки додатні значення й звертається в нуль
при ![]() . Отже, розглянута функція є додатною
визначеною.
. Отже, розглянута функція є додатною
визначеною.
Приклад 2. Функція ![]() від’ємних значень не приймає, але в нуль
звертається не тільки в точці
від’ємних значень не приймає, але в нуль
звертається не тільки в точці ![]() , але й у всіх точках
прямій
, але й у всіх точках
прямій ![]() (поверхня торкається площини
(поверхня торкається площини ![]() по прямій
по прямій ![]() ). Отже,
ця функція знакопостійна (додатна), але не знаковизначена.
). Отже,
ця функція знакопостійна (додатна), але не знаковизначена.
Приклад 3. Функція ![]() буде очевидно знакозмінною.
буде очевидно знакозмінною.
Розглянемо функцію Ляпунова ![]() . Її аргументи
. Її аргументи ![]() , будучи варіаціями, являють собою функції
, будучи варіаціями, являють собою функції ![]() , що задовольняють рівнянням збуреного руху
(3.56), де
, що задовольняють рівнянням збуреного руху
(3.56), де
![]() ,
, ![]() (3.59)
(3.59)
Але тоді ![]() буде складною функцією часу
буде складною функцією часу ![]() .
.
Ознака 1. Повна похідна за часом функції Ляпунова в точці рівноваги дорівнює нулю.
Дійсно, використовуючи правило диференціювання складної функції й рівняння (3.56), знаходимо
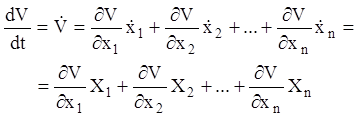 . (3.60)
. (3.60)
Звідси в силу (3.59)одержуємо
![]() (3.61)
(3.61)
Ознака 2. Нехай ![]() - безперечно додатна функція й
- безперечно додатна функція й ![]() – від’ємний параметр. Тоді поверхня
– від’ємний параметр. Тоді поверхня
![]() (3.62)
(3.62)
замкнута й містить усередині себе початок координат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.