Стійкість нелінійних систем. Методи Ляпунова. Функції Ляпунова. Їхні основні властивості. Теореми Ляпунова

3.8 Стійкість нелінійних систем. Методи Ляпунова

Розглянемо тепер методи досліджень стійкості нелінійних систем. Ці методи розділені А. М. Ляпуновим на дві категорії. До першої категорії віднесені методи й прийоми дослідження систем на стійкість, які використовують розв'язання цих систем або їхньої оцінки. Сукупність способів першої категорії в літературі називають першим методом Ляпунова. До іншої категорії Ляпунов відніс методи й прийоми, які використовують непрямі ознаки, по яких установлюється стійкість точки спокою систем. Сукупність способів і прийомів іншої категорії називають у літературі другим методом Ляпунова.

Дослідження стійкості по першому наближенню

Нехай праві частини нелінійної динамічної системи

                                               (3.47)

є неперервними функціями разом зі своїми частинними похідними до другого порядку включно. Тоді використовуючи формулу Тейлора, систему (3.47) можна представити у вигляді

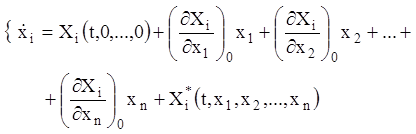                                (3.48)

Якщо покласти, що 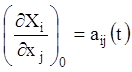 й урахувати, що , то одержимо

,                             (3.49)

де  містять члени не нижче другого порядку відносно , тобто є малими вищих порядків у порівнянні з лінійними членами.

Система лінійних рівнянь

, ,                                      (3.50)

отримана із системи (3.49) відкиданням в останньої нелінійних членів , називається вкороченою системою або системоюрівнянь першого наближення. При цьому виникає питання: при яких умовах, досліджуючи на стійкість систему (3.49), її можна замінити вкороченою системою (3.50).

А.М. Ляпуновим було доведено, що збіг згаданих результатів для систем (3.49) і (3.50) буде в тих випадках, коли нульове розв'язання вкороченої системи або асимптотично стійке, або нестійке. Якщо ж нульове розв'язання системи першого наближення (3.50) стійке, але не асимптотично, то нульові розв'язання систем (3.49) і (3.50) відносно стійкості можуть поводитися по різному. Останній факт особливо наочний у випадку системи другого порядку. У випадку не асимптотичної стійкості руху такої системи фазові траєкторії залишаються в як завгодно малій околиці точки рівноваги, однак точка, що зображує, не прагне до неї (вона коливається біля стану рівноваги, не прагнучи до нього). Але тоді через необмеженість часу починають впливати відкинуті нелінійні члени вищого порядку малості, які можуть спотворити картину й порушити стійкість.

У світі тут сказаного, мають місце наступні теореми про стійкість по першому наближенню.

Нехай нелінійну систему (3.47) можна представити у вигляді (3.49) або в матричній формі

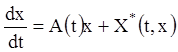,                                                           (3.51)

де  – деяка матриця,  – функція, що задовольняє нерівності

,                                                          (3.52)

с постійною  досить малої в околиці нуля . Цій умові задовольняє будь-яка функція, що має рівномірно неперервні при ,  похідні по змінній . Система першого наближення в цьому випадку має вигляд

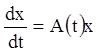.                                                                   (3.53)

Тоді має місце теорема:

Теорема. Якщо фундаментальна матриця  розв'язань системи першого наближення (3.53) при будь-яких ,  задовольняє нерівності

                                                              (3.54)

с додатними постійними  й , то нульове розв'язання системи (3.51) асимптотично стійке при будь-якому виборі функції , що задовольняє нерівності (3.52) з постійними , меншими , причому будь-яке розв'язання  системи (3.51) для якого  задовольняє нерівності

.                                                         (3.55)

Очевидно, що якщо умова (3.52) виконується у всьому фазовому просторі, то ця теорема гарантує для точки спокою системи (3.51) асимптотичну стійкість у цілому (при будь-яких початкових збуреннях)

Зокрема, для системи (3.51), що має стаціонарне перше наближення (3.53) (), її точка спокою за умови (3.52) асимптотично стійка, якщо дійсні частини всіх коренів характеристичного рівняння системи (3.53) від’ємні. Можна показати, що якщо дійсна частина хоча б одного характеристичного числа системи (3.53) додатна, то при цьому точка спокою нелінійної системи (3.47) нестійка. Якщо система (3.53) тільки стійка, то про характер точок спокою системи (3.51) нічого певного сказати не можна: вона завдяки впливу нелінійного доданка  в (3.51) може виявитися як стійкою, так й асимптотичне стійкою, так і нестійкою. Таким чином мають місце наступні теореми про стійкість нелінійних автономних систем по першому наближенню:

Теорема 1. (про стійкість руху): Якщо дійсні частини всіх коренів характеристичного рівняння системи першого наближення від’ємні, то незбурений рух стійкий асимптотично незалежно від виду членів вищих порядків малості в диференціальних рівняннях (3.51) обуреного руху.

Теорема 2. (про нестійкість руху): Якщо серед коренів характеристичного рівняння системи першого наближення найдеться хоча б один з додатною дійсною частиною, то незбурений рух нестійкий незалежно від виду членів вищих порядків малості в диференціальних рівняннях (3.51) збуреного руху.

Теорема 3: Якщо характеристичне рівняння системи першого наближення не має коренів із додатними дійсними частинами, але має корені із дійсними частинами, рівними нулю, то залежно від виду членів вищих порядків малості в диференціальних рівняннях збуреного руху незбурений рух може бути  або стійким, або нестійким.

Розглянемо кілька прикладів:

Приклад 1: Дослідити стійкість збуреного руху

,

Розв’язання: Записуємо систему першого наближення, відкидаючи в правих частинах рівнянь члени степеня вище першої: