Неопределенный интеграл. Основные методы интегрирования. Интегрирование рациональной дроби

Неопределенный интеграл.

Основные определения и свойства.

Функция  называется первообразной функцией (или просто первообразной) для функции  на интервале , если в любой точке  этого интервала функция  дифференцируема и имеет производную ­, равную .

     ,    .

Теорема. Если  - любые первообразные для функции  на интервале , то всюду на этом интервале , где -некоторое частное.

Положим . Так как каждая из функций  дифференцируема на интервале , то по свойству производной дифференцируема и разность  на интервале . При этом , то есть , что требовалось доказать.

Следствие. Если -одна из первообразных для функции  на интервале , то любая первообразная  для функции  на интервале  имеет вид

.

То есть, меняя постоянную , получаем все множество первообразных для функции  на интервале .

Совокупность всех первообразных функций для функции  на интервале  называется неопределенным интегралом от функции  на этом интервале и обозначается символом , где знак ò-знак интеграла, - подынтегральное выражение, функция -подынтегральная функция.

В силу следствия предыдущей теоремы имеем

=

отметим следующие свойства.

= , =, то есть знаки  и  взаимно сокращаются. Действительно, по определению имеем:

= и, взяв дифференциал, получим

=, где в последнем соотношении использовано определение первообразной  .

Во втором свойстве = использовано также определение первообразной   или .

Еще одним свойством является следующее

С точностью до постоянного множителя.

Действительно, пусть функция  имеет первообразную , а функция  первообразную : , .Тогда

 и функция  является первообразной для функции , что и требовалось доказать.

И, наконец,

так  как функция  имеет первообразную   то

, откуда ясно, что функция - первообразная

Для функции .

Для определения первообразной и неопределенного интеграла позволяют нам составить таблицу основных неопределенных интегралов по следующему правилу: производная правой части равна подынтегральной функции левой части.

1.  2.

3.  

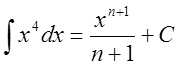
4.,   

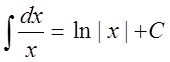5.

6.

7.

8., 

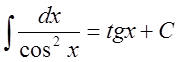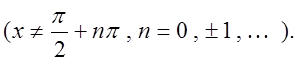
9. ,

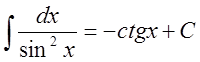10.   

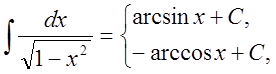
11.

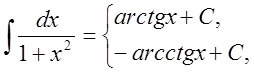
12., 

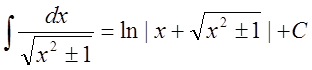13.,    .

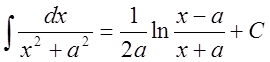В результате построения этой таблицы интегралов можно предположить, что интегралы от элементарных функций также являются элементарными функциями (как это имеет место для производных функций). Однако, что неверно. В качестве примеров рассмотрим некоторые неопределенные интегралы, не имеющие первообразных среди элементарных функций:

  -   интеграл Пуассона,

или

-интеграл Френеля,

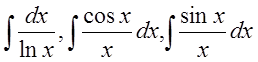-интегральные логарифм, косинус и синус. Каждый из этих интегралов представляет неэлементарную функцию.

Основные методы интегрирования.

1.  Интегрирование заменой переменных (подстановкой).

Теорема. Пусть функция  определена и дифференцируема на некотором множестве  и пусть  - множество всех значений этой функции. Пусть также для функции  существует на множестве    первообразная  , то есть Тогда, всюду на множестве  для функции существует первообразная функция  , то есть

Доказательство основано на определении первообразной. Покажем , что производная  равна . Действительно, функция  -сложная функция и производная от нее равна

.В последнем соотношении использовано определение первообразной.

2.  Интегрирование по частям . 

Теорема. Пусть каждая из функций  дифференцируемы на множестве  и, кроме того, на это множестве  существует первообразная для функции    . Тогда на множестве   существует первообразная для функции  и имеет место формула

Для доказательства теоремы запишем формулу производной произведения

    ,

Умножим ее на   и возьмем интеграл от обоих частей равенства. Так как имеются первообразные на множестве   и ,то на этом же множестве существует первообразная  и имеет место искомое соотношение 

Так как , то имеем другую форму интегрирования по частям

Практика показывает, что большая часть интегралов, берущихся по частям, может быть разбита на три группы:

1) К первой группе относятся интегралы, подынтегральная функция которых содержит в качестве множителя одну из функций

 или их степени. В этой группе полагаем, что  равна одной из указанных функций.

2) Ко второй группе относятся интегралы вида

,

где   -действительные постоянные,  -  любое целое положительное число. Интегралы этой группы берутся   -  кратным применением формулы интегрирования по частям, причем, всякий раз за   принимается степенная функция.

3) К третьей группе относятся интегралы вида

Приравняв любой из интегралов , и произведя двукратное интегрирование по частям, составим для  уравнение первого порядка. Приведем несколько примеров на теоремы интегрирования.

Интегралы, содержащие иррациональные выражения вида

Имеют первообразные в следующих случаях:

а) 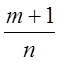   -целое число,  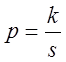-дробное число. Тогда по методу замены переменной

Например,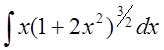

Здесь  . Подставляя вместо  новую переменную  , имеем

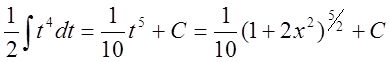
б) 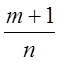   - не является целым числом, 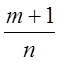+   -целое число. В этом случае

Например,

Здесь   

Подставив вместо  новую переменную, получим

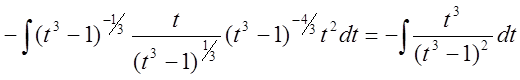
Упростим полученный интеграл, используя теорему об интегрировании по частям.

Положим    и 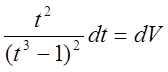 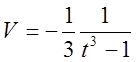       и имеем:

Интеграл 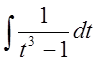 вычислим позднее.