Неопределенный интеграл. Основные методы интегрирования. Интегрирование рациональной дроби, страница 3

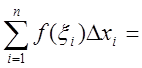
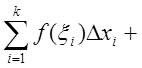
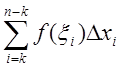   , где 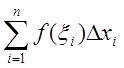   - интегральная сумма функции  при ,  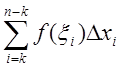- интегральная сумма функции  при  

Присвоим  - ому интервалу номер

Тогда имеем

,

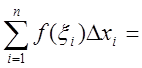
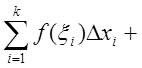
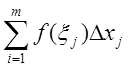чему соответствует рассматриваемое равенство.

Основные теоремы.

Теорема 1.

Если  на интервале , то на этом интервале

     

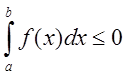
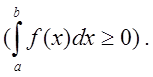
Пусть . Тогда 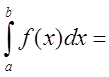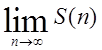, где  - интегральная сумма. Пусть также 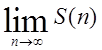 или . Очевидно, что при   число  положительным быть не может:

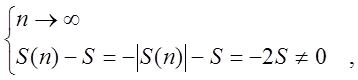
что и требовалось доказать.

Теорема 2. Если на интервале  выполняется неравенство  , то имеет место оценка интеграла

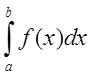
Неравенство  можно записать в виде

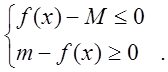
Применив к ним предыдущую теорему, получим

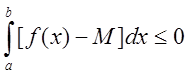
  или, согласно свойствам интеграла:

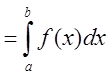
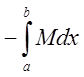
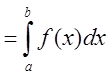
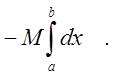
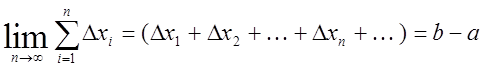
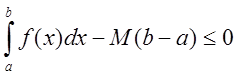- длина отрезка, то  или 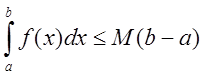. Точно также получим 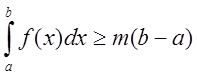, что и требовалось доказать.

Средним значением определенного интеграла 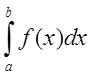  называется число, равное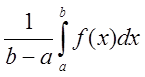 

Теорема о среднем значении определенного интеграла.

Пусть существует 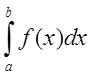  и   - наименьшее и наибольшее значения функции  при   . Тогда найдется такое число            , что

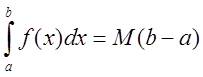
Так как  , то по теореме 2 имеем

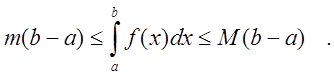
Разделив на  , получим

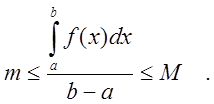
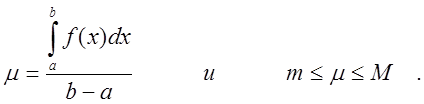
Здесь – значение непрерывной функции в фиксированной точке.

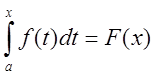   называется интегралом с переменным верхним пределом для функции   непрерывной при    

Такой интеграл является функцией верхнего предела и поэтому обозначен как .

Теорема. Любая непрерывная на интервале  функция  имеет на этом интервале первообразную. Одной из таких первообразных является интеграл с переменным пределом

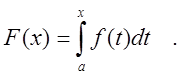
Требуется доказать, что между функциями  и  при   имеет место равенство 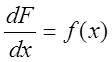. По определению производной имеем

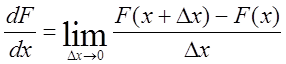
, где           

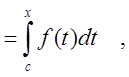
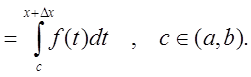
По теореме о среднем значении

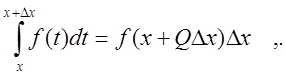где   заключено между .

Тогда

               

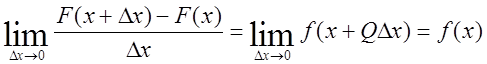
в силу непрерывности  .

Формула Ньютона-Лейбница.

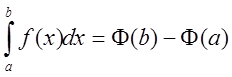  -  основная формула интегрального исчисления,                        - первообразная для функции  на интервале .

Согласно предыдущей теореме

 .

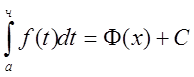Положим       . Тогда 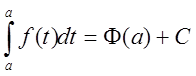   или 

                  .                 .

Положим        .Тогда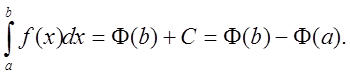

Теорема о замене переменной в определенном интеграле.

Пусть функция  непрерывна на замкнутом интервале , который является множеством значений функции ,

определённой для  и имеющей на этом множестве непрерывную производную. Кроме того, , .

Тогда имеет место формула

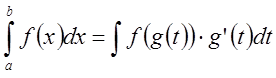
Рассмотрим одну из первообразных  функции . По формуле Ньютона-Лейбница имеем 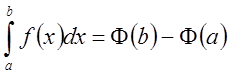 и покажем, что правая часть такая же. Возьмём функцию  и продифференцируем её:

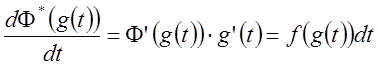, где использовано определение первообразной по аргументу : .

Тогда функция  – первообразная для подынтегральной функции  и по формуле Ньютона-Лейбница получим

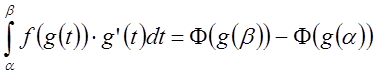 или согласно условию теоремы

.

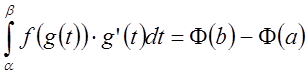Теорема об интегрировании по частям.

Пусть функции  и  имеют непрерывные производные на множестве . Тогда имеет место формула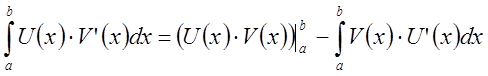

Так как , то эту формулу можно записать .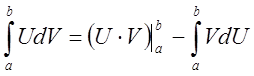

Легко видеть, что функция  является первообразной для функции  и по формуле Ньютона-Лейбница

.

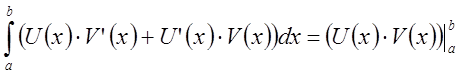Отсюда и получается искомое выражение.

Геометрические положения определённого интеграла.

1.  Площадь криволинейной трапеции.

Пусть на множестве  задана непрерывная или кусочно-непрерывная функция , графиком которой является некоторая линия. Проведём две прямые  и ,  и получим криволинейную трапецию, образованную заданной линией, прямыми ,  и отрезком оси абсцисс . Составим интегральную сумму 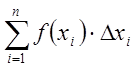, где  – площадь i-ой криволинейной трапеции. Тогда, согласно определению определённого интеграла получим

,

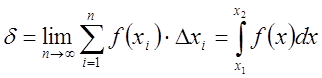 при  и  – элемент площади – бесконечно малая величина первого порядка.

2.  Длина линии.

А) Декартово задание функции.

Пусть на множестве , задана функция , имеющая внутри этого множества непрерывную производную. Тогда на декартовой координатной проекции имеем линию, длина которой  неизвестна.

Разобьем линию на  частей, длина каждого из которых . Проведём прямые ,  и при их пересечении с линией получим точки с координатами  и , .

Проведя через точку  прямую , получим криволинейный треугольник со сторонами, равными  и . Соединив отрезком прямой точки , получим прямоугольный треугольник с гипотенузой, равной

Суммируем длины участков линии

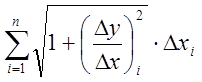. Переходя к пределу при  и  (или ), получим по определению определённого интеграла длину линии :