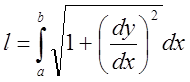 , где
, где 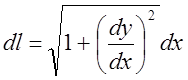 – элемент (бесконечно малая величина
первого порядка) длины линии.
– элемент (бесконечно малая величина
первого порядка) длины линии.
Б) Параметрическое задание функции.
Пусть на множестве точек ![]() задана функция
задана функция 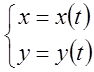 .
Требуется вычислить длину линии
.
Требуется вычислить длину линии ![]() . Поскольку
. Поскольку 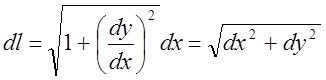 и
и ![]() ,
, ![]() , то
, то
![]() и
и 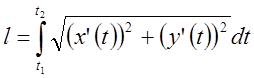 .
.
3. Объём тела вращения.
Пусть функция ![]() непрерывна на множестве
непрерывна на множестве ![]() , тогда объём
, тогда объём ![]() тела,
образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной
графиком функции
тела,
образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной
графиком функции ![]() , ординатами в точках a и b и
отрезком оси Ох от a до b может быть найден по формуле
, ординатами в точках a и b и
отрезком оси Ох от a до b может быть найден по формуле
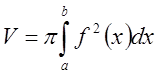 .
.
Действительно, при вращении
этой трапеции около оси абсцисс каждая точка ![]() этой
оси является центром круга, а ордината
этой
оси является центром круга, а ордината ![]() –
радиусом этого круга. Площадь круга при этом равна
–
радиусом этого круга. Площадь круга при этом равна ![]() . Умножив последнюю величину на
. Умножив последнюю величину на ![]() , получаем величину объема цилиндрического тела
, получаем величину объема цилиндрического тела ![]() . Для нахождения объёма составим
интегральную сумму
. Для нахождения объёма составим
интегральную сумму
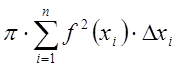 и при
и при
![]() получим
получим
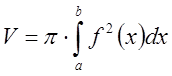 .
.
Несобственные интегралы с бесконечными пределами.
Пусть функция ![]() определена в промежутке
определена в промежутке ![]() и
и 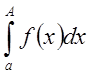 в
любой его части
в
любой его части ![]() имеет смысл при любом
имеет смысл при любом ![]() .
.
Если при ![]() для этого интеграла существует
определённый конечный предел, то его называют интегралом функции
для этого интеграла существует
определённый конечный предел, то его называют интегралом функции ![]() в промежутке от
в промежутке от ![]() до
до
![]() и обозначают символом
и обозначают символом 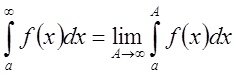 .
.
В этом случае говорят, что
интеграл существует или сходится. В отличие от определённого (собственного)
интеграла только его введённый интеграл называется несобственным. Если предел 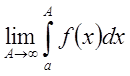 бесконечен или не существует, то говорят,
что несобственный интеграл не существует или расходится.
бесконечен или не существует, то говорят,
что несобственный интеграл не существует или расходится.
Аналогично определяется, 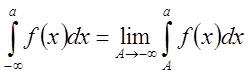 равно как и интеграл функции
равно как и интеграл функции ![]() от -∞ до ∞:
от -∞ до ∞:  .
.
Взяв любое a,
положим 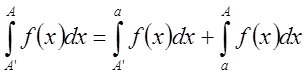 . Переходя к пределу, получим
. Переходя к пределу, получим 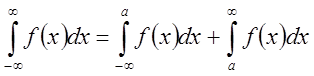 и существование левой части равносильного
существованию обоих интегралов справа.
и существование левой части равносильного
существованию обоих интегралов справа.
Пусть, например, ![]() – непрерывная функция в промежутке
– непрерывная функция в промежутке ![]() и для неё существует первообразная
и для неё существует первообразная ![]() , тогда по формуле Ньютона-Лейбница
, тогда по формуле Ньютона-Лейбница
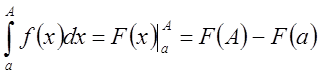
Отсюда,
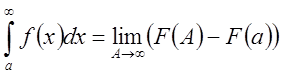 и,
очевидно, что вычисление несобственного интеграла проводится в два этапа:
сначала вычисляется определённый интеграл, затем находится его предел при
и,
очевидно, что вычисление несобственного интеграла проводится в два этапа:
сначала вычисляется определённый интеграл, затем находится его предел при ![]() .
.
Необходимый и достаточный признак сходимости несобственного интеграла с бесконечным пределом от положительной функции.
Для существования
несобственного интеграла 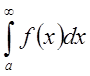 в случае положительной
функции необходимо и достаточно, чтобы интеграл
в случае положительной
функции необходимо и достаточно, чтобы интеграл 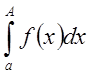 при
возрастании А оставался ограниченным
при
возрастании А оставался ограниченным 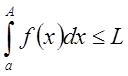 , (
, (![]() ). Если же это условие не выполнено, то
несобственный интеграл равен ∞.
). Если же это условие не выполнено, то
несобственный интеграл равен ∞.
Необходимость. Если 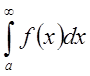 сходится, то выполняется признак
сходится, то выполняется признак 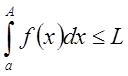 .
.
Так как 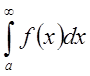 сходится, то по определению существует его
конечный предел, равный ??? L.
сходится, то по определению существует его
конечный предел, равный ??? L.
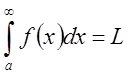 . С
другой стороны, имеет место очевидное неравенство
. С
другой стороны, имеет место очевидное неравенство 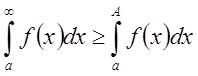 .
Учитывая сходимость, получим искомый признак
.
Учитывая сходимость, получим искомый признак 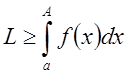 .
.
Достаточность. Если 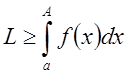 , то
, то 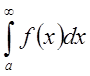 сходится.
Так как
сходится.
Так как 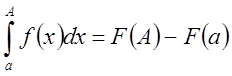 , то по условию теоремы
, то по условию теоремы ![]() – монотонно возрастающая функция (с
увеличением А) и ограниченная, то по признаку существования предела, её предел
при
– монотонно возрастающая функция (с
увеличением А) и ограниченная, то по признаку существования предела, её предел
при ![]() существует и является числом.
существует и является числом.
В противоположном случае, то
есть при 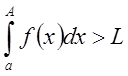 , функция
, функция ![]() , с
увеличением А, становится больше любой сколь угодно большой величиной L или
по определению является бесконечно большой величиной.
, с
увеличением А, становится больше любой сколь угодно большой величиной L или
по определению является бесконечно большой величиной.
Теорема сравнения.
Если, хотя бы при ![]() имеет место неравенство
имеет место неравенство ![]() , то из сходимости интеграла
, то из сходимости интеграла 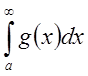 следует сходимость интеграла
следует сходимость интеграла 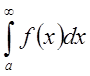 , а из расходимости
, а из расходимости 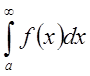 следует
расходимость
следует
расходимость 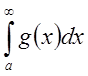 . Так как
. Так как 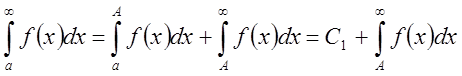 ,
где С1 – величина, равная значению предельного интеграла от функции
,
где С1 – величина, равная значению предельного интеграла от функции ![]() , то сходимость
, то сходимость 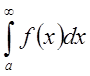 следует
из сходимости
следует
из сходимости 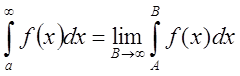 .
.
По условию при ![]()
![]() и
и 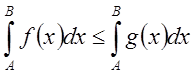 . Поскольку
. Поскольку 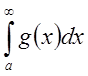 сходится,
то любой интеграл из промежутка
сходится,
то любой интеграл из промежутка ![]() также сходится и
также сходится и  по необходимому и достаточному признаку.
Поэтому и
по необходимому и достаточному признаку.
Поэтому и 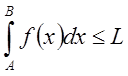 также сходится.
также сходится.
Если же 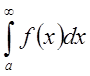 расходится,
то
расходится,
то 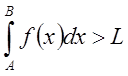 и из неравенства:
и из неравенства: 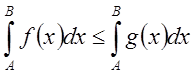 следует
следует 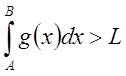 расходимость
расходимость
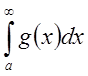 .
.
Несобственные интегралы от неограниченных функций.
Рассмотрим функцию ![]() ,
, ![]() , для
которой существует
, для
которой существует  , то есть этот интеграл является
определённым. В то же время
, то есть этот интеграл является
определённым. В то же время  не существует (
не существует (![]() ). И точка b называется
особой точкой функции
). И точка b называется
особой точкой функции ![]() для
для ![]() .
.
Например, 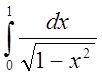 – несобственный интеграл, точка х=1 –
особая точка,
– несобственный интеграл, точка х=1 –
особая точка, 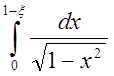 – определённый интеграл при
– определённый интеграл при ![]() .
.
Если для интеграла  при
при ![]() существует
определённый конечный предел, то его называют интегралом функции
существует
определённый конечный предел, то его называют интегралом функции ![]() от a до b и
обозначают
от a до b и
обозначают 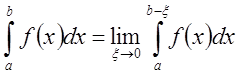 . При этом говорят, что интеграл существует
или сходится. В противном случае говорят, что интеграл не существует или
расходится.
. При этом говорят, что интеграл существует
или сходится. В противном случае говорят, что интеграл не существует или
расходится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.