Таким чином,
тривимірна задача теорії пружності після застосування перетворення Лапласа
зводиться до находження функції двох замінних ![]() Подальший
розгляд цієї задачі виходить за межі цього посібника.
Подальший
розгляд цієї задачі виходить за межі цього посібника.
2.16 Підсумовування рядів
Розглянемо спосіб застосування перетворення Лапласа для підсумовування рядів.
Нехай треба
знайти суму числового ряду 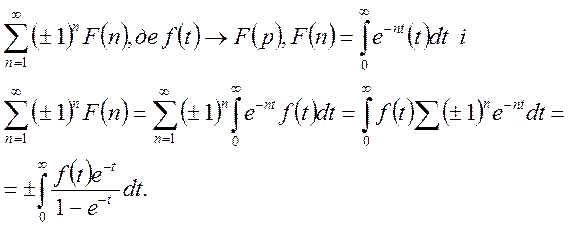
Таким чином, задача про підсумовування рядів зводиться до обчислення невласного інтегралу.
Розглянемо приклад.
Приклад. Знайти суму
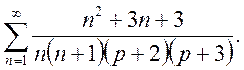
Маємо 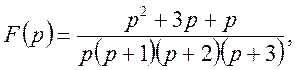
де ![]() - прості полюси.
- прості полюси.
Застосовуючи формулу розкладання (39) знайдемо
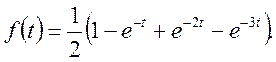
Тоді
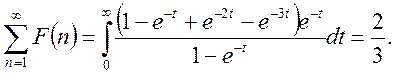
Вправи. Знайти суми рядів:
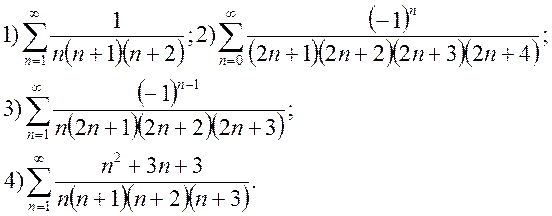
2.17 Таблиця перетворень Лапласа
Таблиця 1
|
№ Оригінал Зображення |
1. 
2. 
3. 
4. 
5. 
6.

7. 
8.

9.

10.

11. 
12.

13. 
14.

15.

2.18 Питання для повторення матеріалу
1. Яким умовам повинна відповідати функція – оригінал?
2. Що таке інтегральне перетворення Лапласа?
3. Назвіть область існування перетворення Лапласа?
4. Що таке функція Хевісайда і яке воно має зображення?
5. Сформулюйте теорему лінійності для перетворення Лапласа?
6. В чому суть теореми запізнення, випередження і зсунення? Сформулюйте їх.
7. Як знаходиться зображення у випадку, коли оригінал є періодичною функцією?
8. Як змінюється оригінал при диференціюванні і інтегруванні зображення?
9. Сформулюйте граничні теореми для оригіналу і зображення.
10. Що називається згорткою функцій? Назвіть приклад використання цього інтегралу.
11. Сформулюйте теорему Бореля про згортку оригіналів.
12. Що таке інтеграл Дюамеля? Наведіть приклад використання цього оригіналу.
13. Приведіть формулу обернення.
14. Що є формулою розкладання? Приведить приклад використання цих формул для випадку простих і кратних полюсів.
15. Сформулюйте теорему про множення оригіналів.
16. Опишіть загальну схему використання перетворення Лапласа при розв’язку диференціальних рівнянь та систем.
17. Яким чином використовують перетворення Лапласа при підсумовуванні рядів? Наведіть приклади.
3 ДИСКРЕТНЕ ПЕРЕТВОРЕННЯ
ЛАПЛАСА
3.1 Функції цілочислового аргументу
Розглянемо функції f(k), аргумент яких є цілі числа
к=0, 1, 2, ... . Для того , щоб до цих
функцій застосувати перетворення Лапласу, їх необхідно подовжити на весь
інтервал ![]() З усіх можливих способів такала
продовження зупинимось на одному.
З усіх можливих способів такала
продовження зупинимось на одному.
Позначимо символом ![]() - найбільше ціле число, що не
перевищує t. Наприклад,
- найбільше ціле число, що не
перевищує t. Наприклад, ![]() Кожній функції f(k) поставимо у відповідність східчасту функцію f([t]), що визначена на
числовому інтервалі
Кожній функції f(k) поставимо у відповідність східчасту функцію f([t]), що визначена на
числовому інтервалі ![]() Для скорочення запису
замість f([t]) будемо писати f[t].
Для скорочення запису
замість f([t]) будемо писати f[t].
Графіки функцій f(k) і f(t) показані на рис. 1 і рис. 2 відповідно.
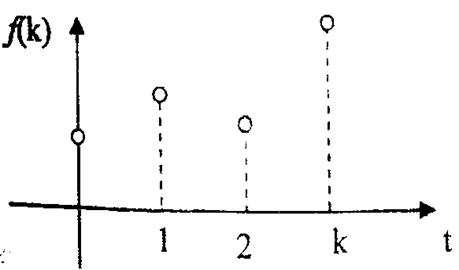
Рис.1
Рис. 2
З означення випливає, що в точках t=k=0, 1, 2, …f[t]=f(k). В той же час, кожній функції f[t] можна поставити у відповідність східчату
функцію f[t] і функцію цілочислового аргументу f(k). Очевидно, що кожну функцію f(k) можна розглядати
як числову послідовність ![]()
Функцію числового аргументу називають також решітковими функціями.
Приклад 1. Позначимо через f(k) суму дільників
числа k. Так ![]()
Означення. Скінченою різницею першого порядку будемо називати решіткову функцію виду
![]() (1)
(1)
Різниці більш високих порядків утворюються за допомогою рекурентних співвідношень
![]() (2)
(2)
Вважаємо ![]()
ТЕОРЕМА.
Скінченні різниці m-ого порядку
визначаються через значення решіткової функції ![]() по
формулі
по
формулі
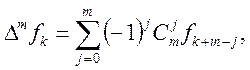 (3)
(3)
де 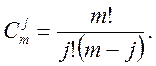
Доведення. Доведення теореми проведемо методом математичної індукції. При m=1 співвідношення (3) має вигляд (1).
Нехай (3) доведено при m=l. Доведемо, що формула (3) має місце при m=l+1. Будемо мати
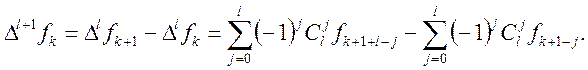
Збираючи коефіцієнти при однакових ![]() і скориставшись рівністю
і скориставшись рівністю ![]() одержимо потрібний вираз для
величини
одержимо потрібний вираз для
величини ![]()
Теорему доведено.
Як частинний випадок запишемо формули
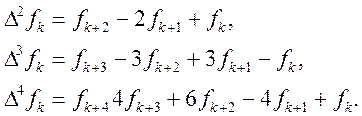
ТЕОРЕМА 2. значення решіткової функції визначаються через скінченні різниці по формулі
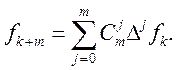 (5)
(5)
Доведення. При m=1 формула (5) випливає із формули (1)
![]()
Далі
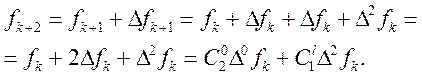
Нехай формула (5) має місце при m=l
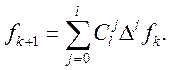
Доведемо, що вона справедлива й при m=l+1. Маємо
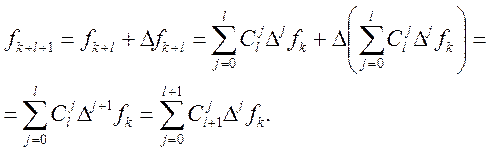
Теорему доведемо.
Приклад 2. Знайдемо скінчену різницю m-ого порядку від узагальненої степеневої функції
![]()
Будемо мати
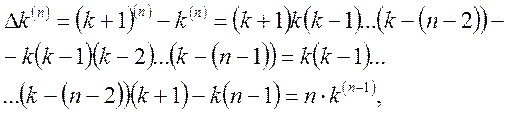
або ![]()
![]()
Далі, застосовуючи метод математичної індукції, можна довести, що
![]() (6)
(6)
Очевидно, що ![]() при m>n.
при m>n.
Вправа.
Знайти ![]()
3.2 Означення дискретного перетворення Лапласа
Розглянемо
решіткову функцію ![]()
Означення.
Дискретним перетворенням Лапласа (D - перетворенням) називається функція комплексної змінної
![]() що визначається рядом
що визначається рядом
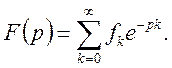 (7)
(7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.