Лінійне різницеве рівняння mго порядку може бути записано у вигляді
Δmfk + b1Δm1fk +...+ bmfk = gk (36)
Використовуючи формули (3), (5) можна перейти від рівняння (36) до рівняння (35) і навпаки.
За допомогою дискретного перетворення Лапласа можна розв’язувати і системи різницевих рівнянь з постійними коефіцієнтами.
Приклад 1. Визначити порядок різницевого рівняння
Δ3fk+2Δ2fk+3Δfk+2fk=3k
Відповідно до формули (1), (4)
Δfk = fk+1 fk
Δ2fk = fk+2 2fk+1 + fk
Δ3fk = fk +3 3fk+2+3f(k+1) fk
Внаслідок маємо
fk+3 fk+2+2fk+1=3k
або після заміни n = k+1
fn+2 Fn+1+2fn = 3n1
Отже дане рівняння другого порядку.
Приклад 2. Знайти розв’язок різницевого рівняння 2fk+2
5fk+1 + 2fk=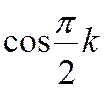 при початкових умовах f0 = f1 = 0
при початкових умовах f0 = f1 = 0
Маємо
fk → F(p)
fk+1 → epF(p),
fk+2 → e2pF(p),
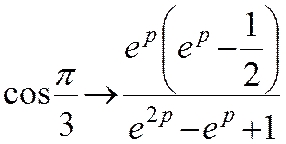
Операторне рівняння для функції F(p) має вигляд
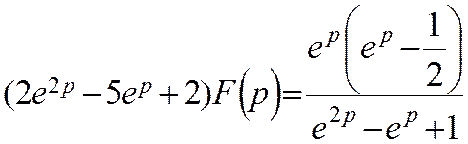
Звідси
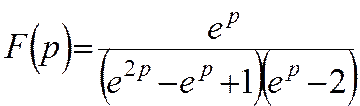
Застосовуючи до функції F(p) спосіб невизначених коефіцієнтів, маємо
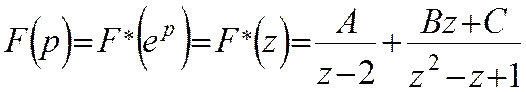
Знаходячи коефіцієнти А,В, С, отримаємо
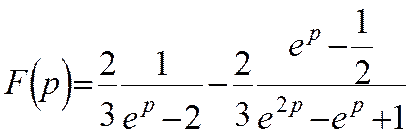
Відомо, що
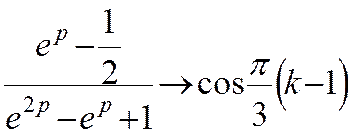 ,
,
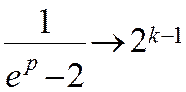
Отже
![]()
fk = 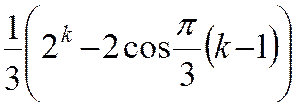
Приклад 3. Знайти загальний член послідовності чисел Фібоначчі: 0, 1, 1, 2, 3, 5, 8,..., в якій кожний наступний член дорівнює сумі двох попередніх.
Нехай fk – загальний член послідовності числа Фібоначчі. Відповідно до умов прикладу для fk одержимо різницеве рівняння:
fk+2 = fk+1 + fk
при початкових умовах f0 = 0,f1 = 1.
Будемо мати
fk ![]() fk+1
fk+1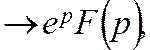 fk+2
fk+2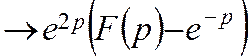
Операторне рівняння
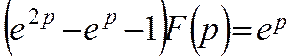
Звідси
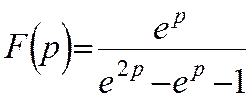
За допомогою способу невизначених коефіцієнтів
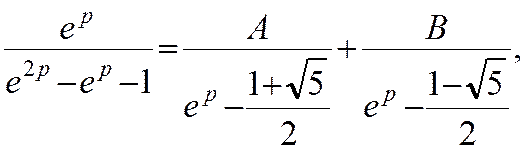
де
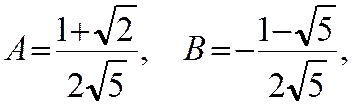
або 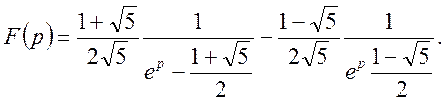
Скориставшись
формулою 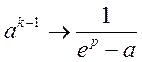 знаходимо
знаходимо
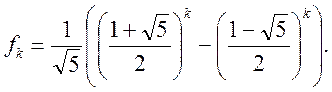
Приклад 4. Знайти розв’язок системи різницевих рівнянь
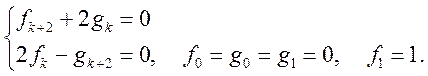
Введемо
позначення ![]()
По теоремі випередження
![]()
Система оперативних рівнянь має вигляд
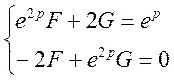
Звідси 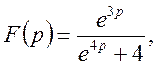
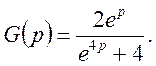
Методом незвичайних коефіцієнтів одержимо
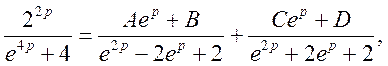
де 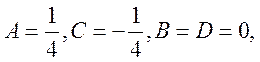 тобто
тобто
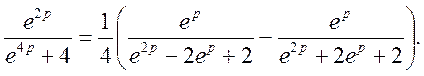
Із відповідності
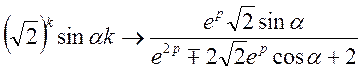
вирливає 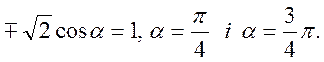
Тому
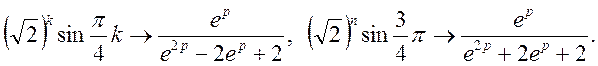
Звідси
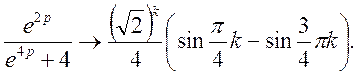
Далі, застосовуючи теорему випередження, маємо
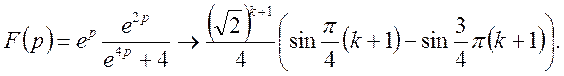
Аналогічно
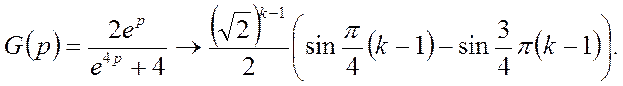
Таким чином,
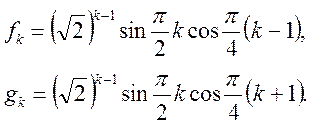
Вправи. Знайти розв’язок різницевих рівнянь чи систем рівнянь:
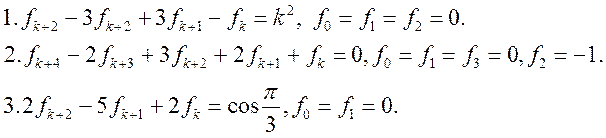
4. Числа 1, 3, 8, 16, … утворюють арифметичну прогресію другого порядку. Це значить, що скінченні різниці другого порядку постійні. Знайти 101 – й член прогресії.
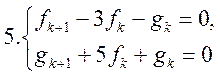
![]()
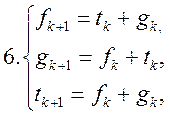
![]()
3.11 Питання для повторення матеріалу
1. Що таке решіткова функція?
2. Що називається скінченою різницею k – ого порядку?
3. Який існує зв’язок між скінченими різницями і решітковими функціями?
4. Що таке дискретне перетворення Лапласа?
5. Яким умовам новина відповідати решіткова функція, щоб було можливе D– перетворення?
6. Як визначається обернене D– перетворення для простих і кратних полюсів зображення F(p)?
7. Які основні властивості D– перетворення Ви знаєте?
8. Сформулюйте теорему про диференціювання і інтегрування зображень.
9. Одержати формулу для зображення скінчених різниць довільного порядку.
10. Що таке функція решіткових функцій?
11. привести приклад використання теореми про суму решіткових функцій для знаходження суми числового ряду.
12. Сформулювати теореми про згортку оригіналів.
13. Що відповідає згортці зображень решіткових функцій?
14. Одержати за допомогою теореми про згортку оригіналів формулу Парсваля.
15. Що таке лінійне різницеве рівняння m– ого порядку?
16. На конкретному прикладі продемонструвати спосіб розв’язку лінійних різницевих рівнянь та систем.
4 СЕМЕСТРОВІ ЗАВДАННЯ
4.1 Семестрове завдання №1
1.Використовуючи теореми лінійності і подібності, знайти зображення функцій:
1) ![]()
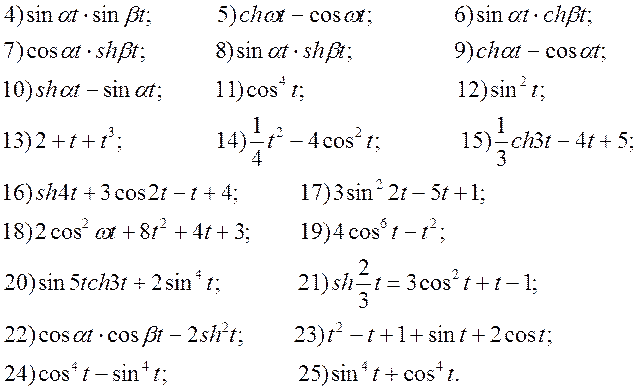
2. Використовуючи теореми запізнення і зсунення, знайти зображення функцій
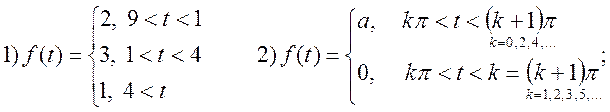
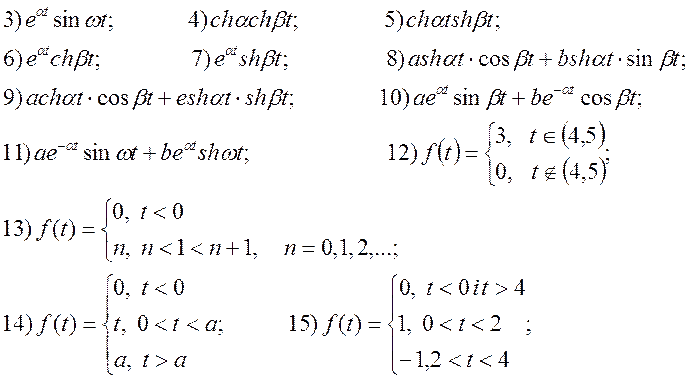
3. Використовуючи теорему по зображення періодичних оригіналів, знайти F(p):
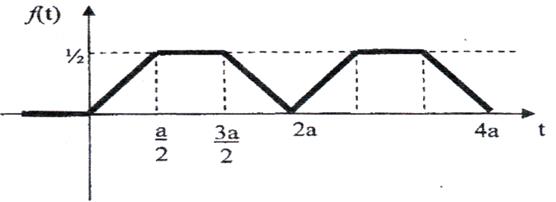 1)
1)
Рис. 1
2)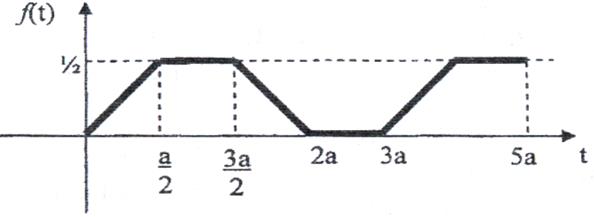
Рис. 2
3) 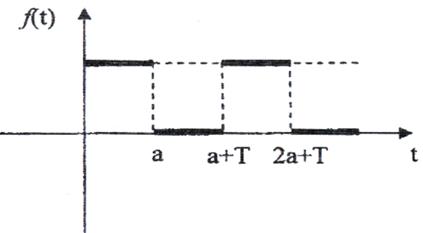
Рис. 3
4)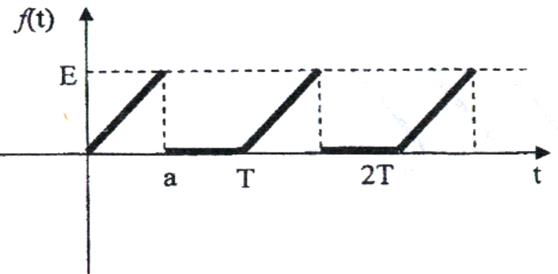
Рис. 4
5) 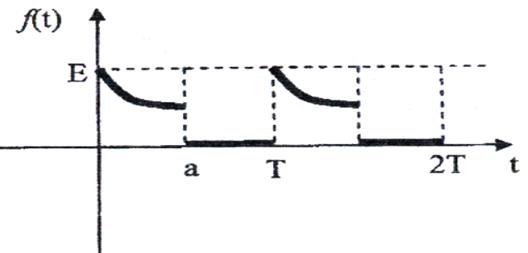
Рис. 5
де 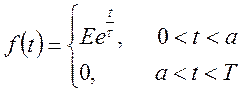
6)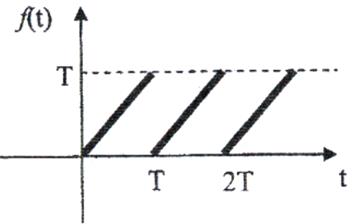
Рис. 6
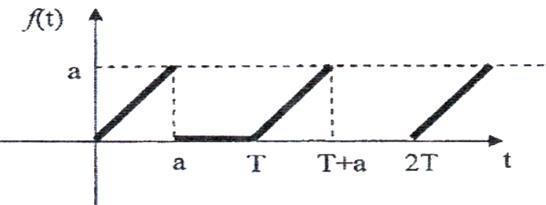 7)
7)
Рис. 7
8) 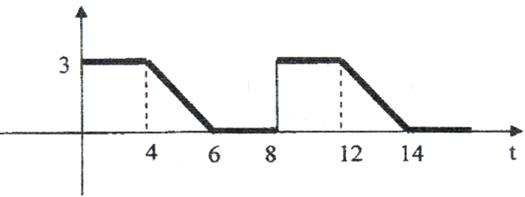
Рис. 8
9)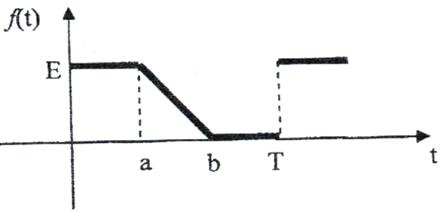
Рис. 9
10)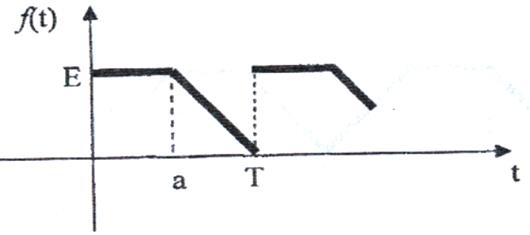
Рис. 10
11)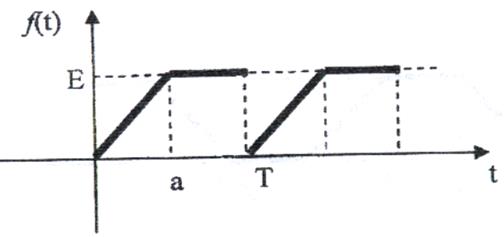
Рис. 11
12)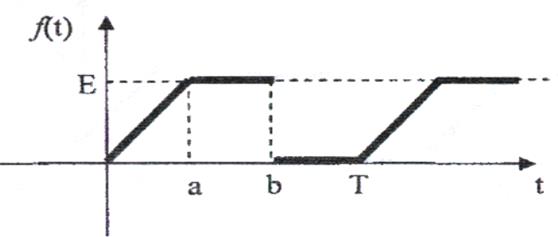
Рис. 12
13)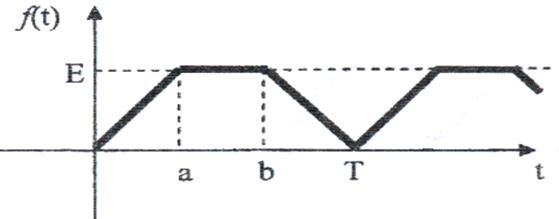
Рис. 13
14) 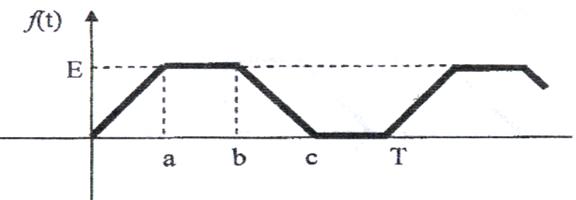
Рис. 14
15)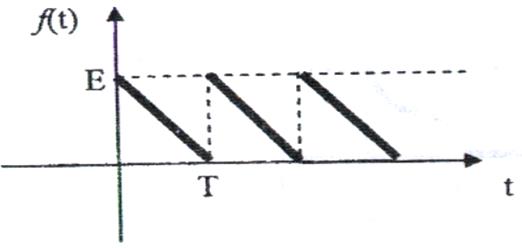
Рис.
15
16) 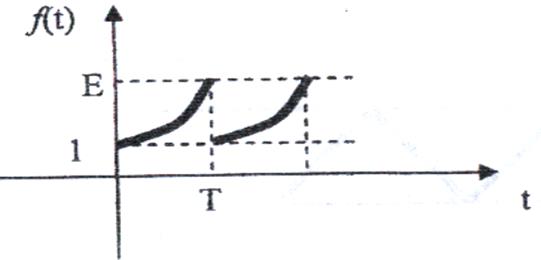
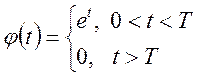
Рис.16
17) 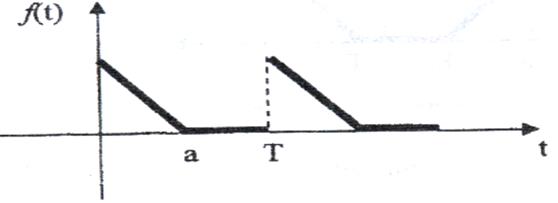
Рис. 17
18)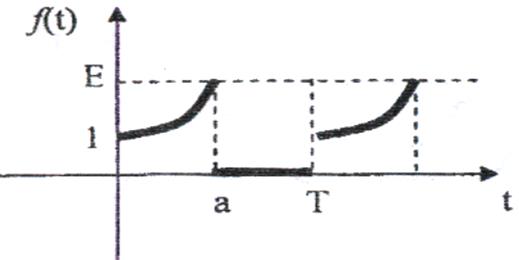
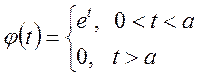
Рис. 18
19) 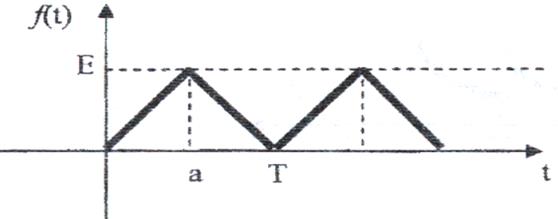
Рис. 19
20) 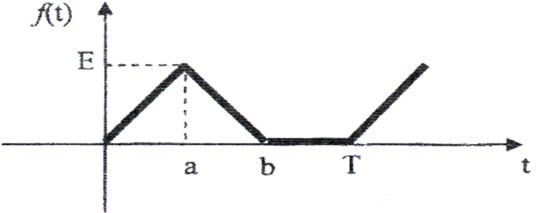
Рис. 20
21) 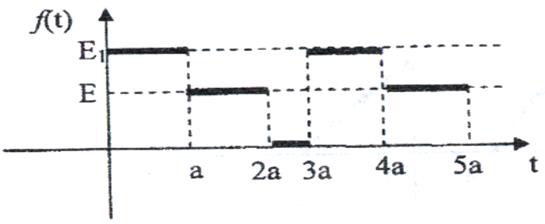
Рис. 21
22) 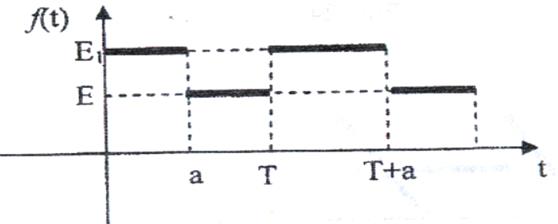
Рис. 22
23) 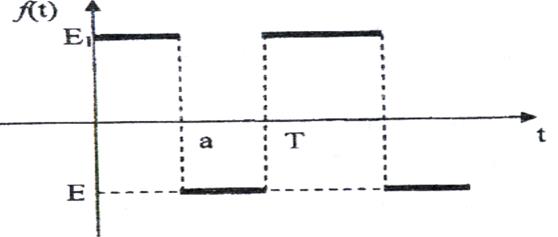
Рис. 23
24) 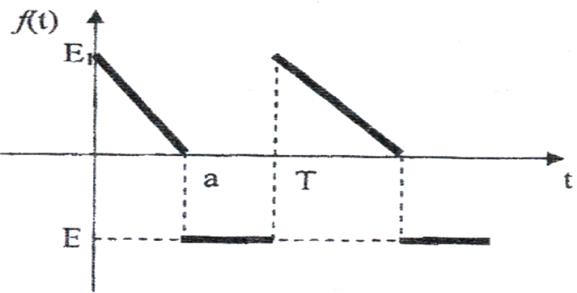
Рис. 24
25) 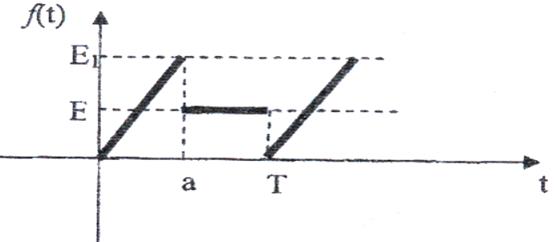
Рис. 25
4. Використовуючи теорему диференціювання оригіналу, найти зображення виразів:
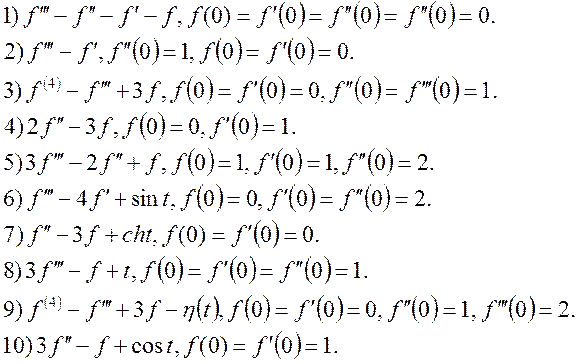
![]()
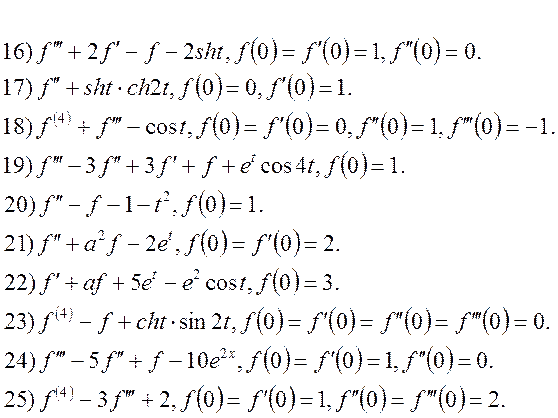
5) Використовуючи теореми інтегрування і диференціювання зображення, знайти зображення функцій:
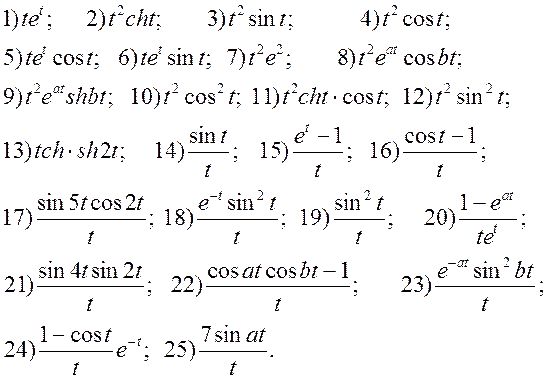
6) Застосовуючи теорему про множення зображень, знайти оригінали для функцій F(p):
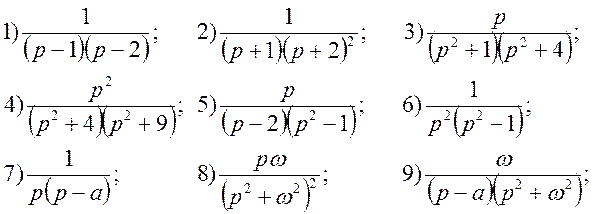
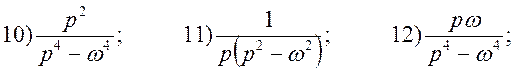
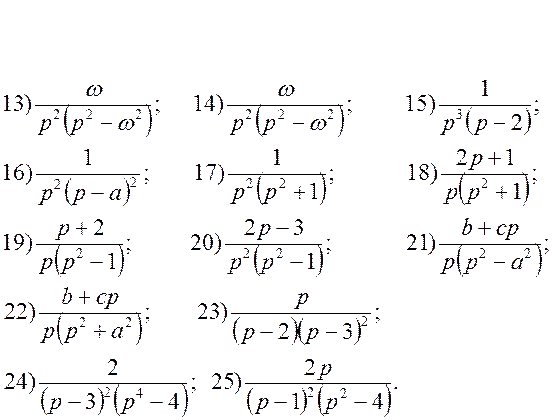
7) Отримати оригінали f(t) для заданих зображень двома способами: а) застосовуючи формули розкладання; б) представляючи функцію F(p) як суму найпростіших дробів.
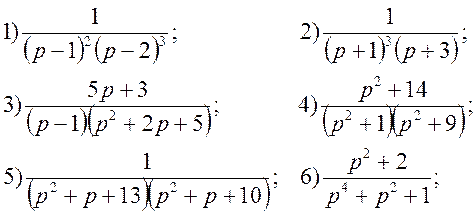
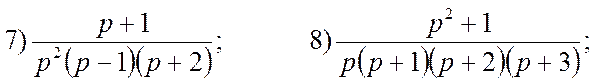
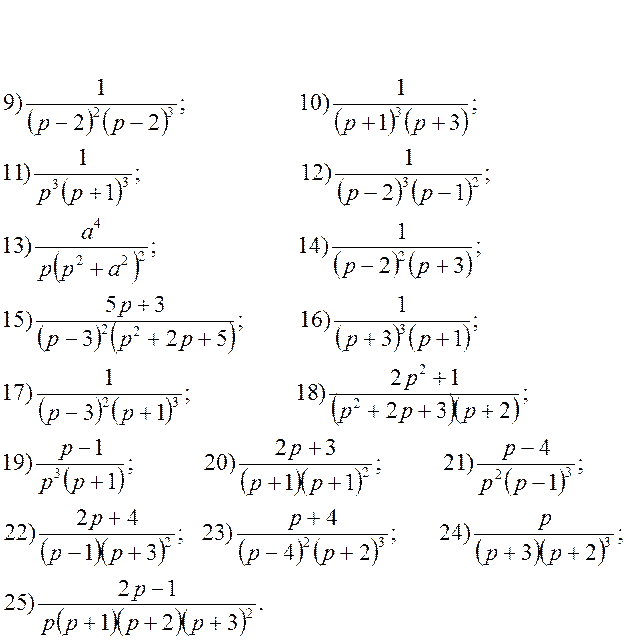
8. Застосовуючи безпосередньо перетворення Лапласа, або за допомогою інтеграла Дюамеля (де мають місце нульові початкові умови), знайти розв’язок диференціальних рівнянь:

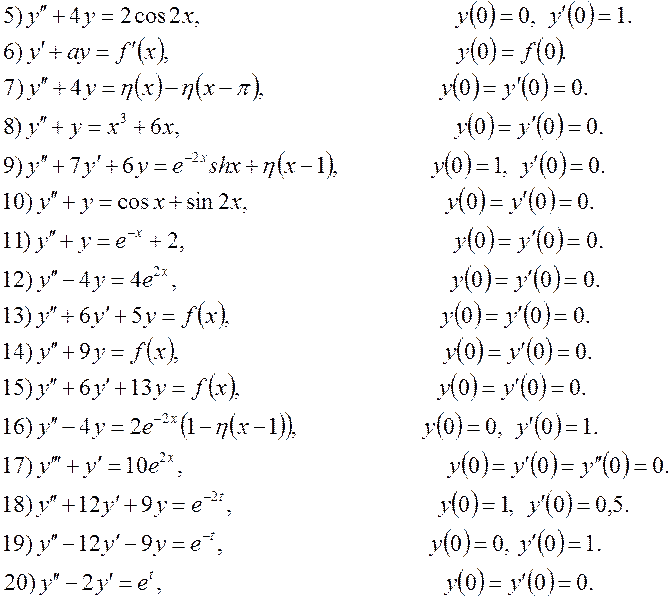
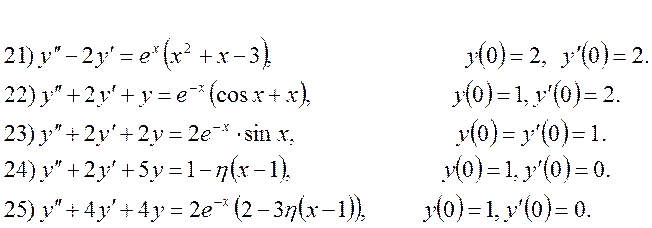
9. За допомогою перетворення Лапласа, знайти розв’язки системи диференціальних рівнянь:
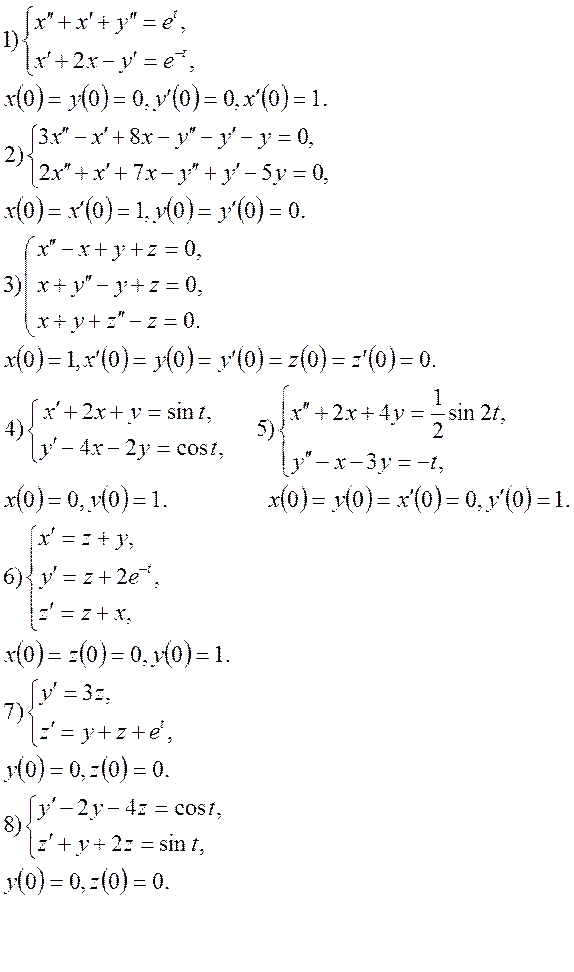
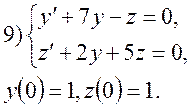
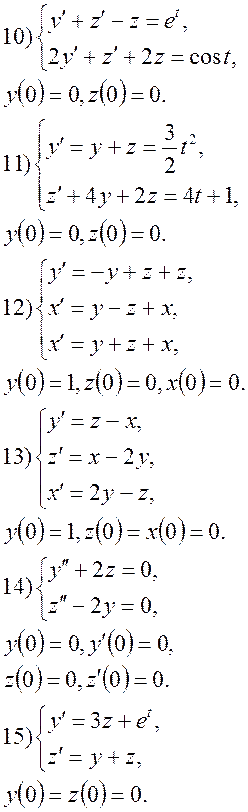
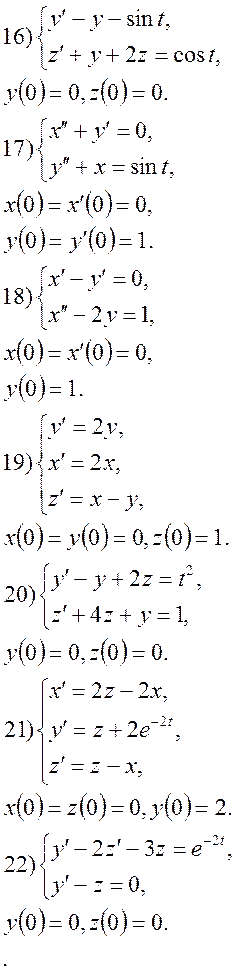
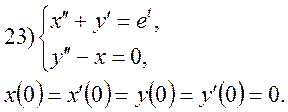
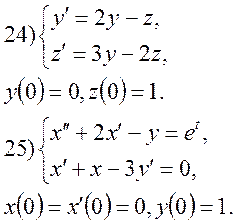
4.2 Семестрове завдання №2
1. Використовуючи формули розкладання,
знайти решіткову функцію ![]() для функції F(p):
для функції F(p):
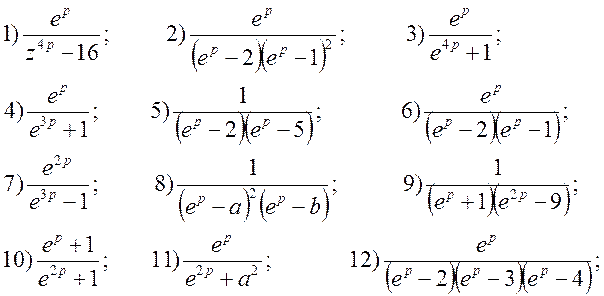
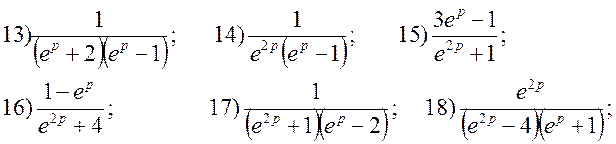
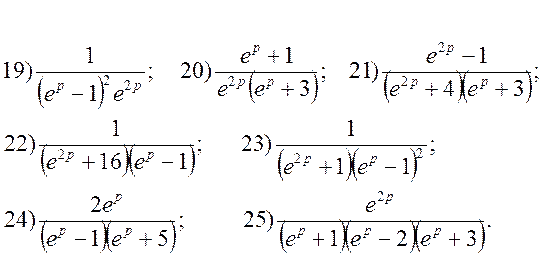
3. Знайти зображення решіткових функцій ![]() :
:
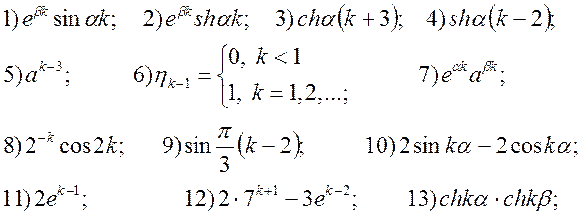
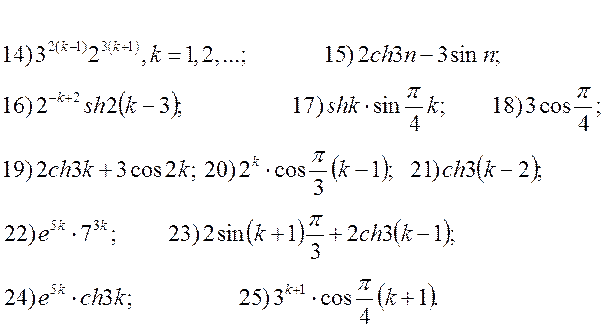
3. застосовуючи теореми диференціювання і інтегрування, знайти зображення для решіткових функцій:
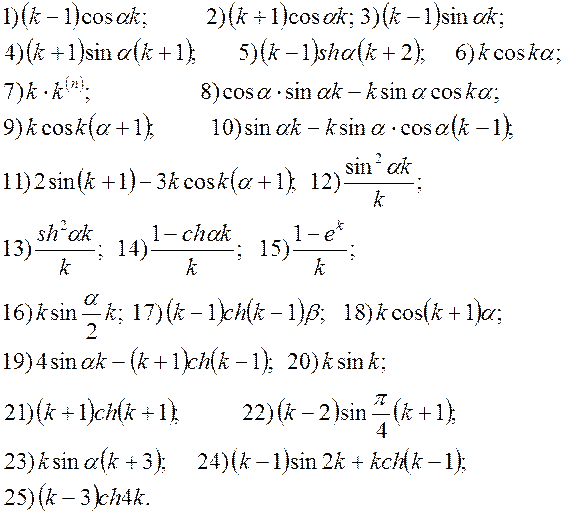
4. Знайти решіткові функцій ![]() шляхом розкладання функцій F(p) на елементарні дроби:
шляхом розкладання функцій F(p) на елементарні дроби:
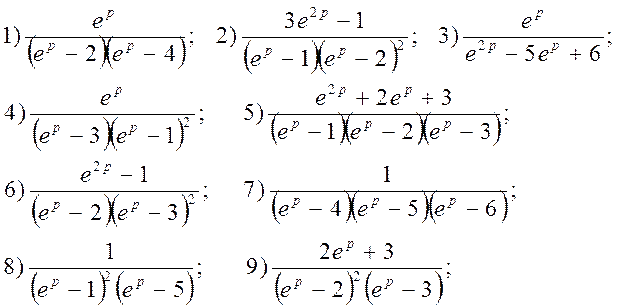
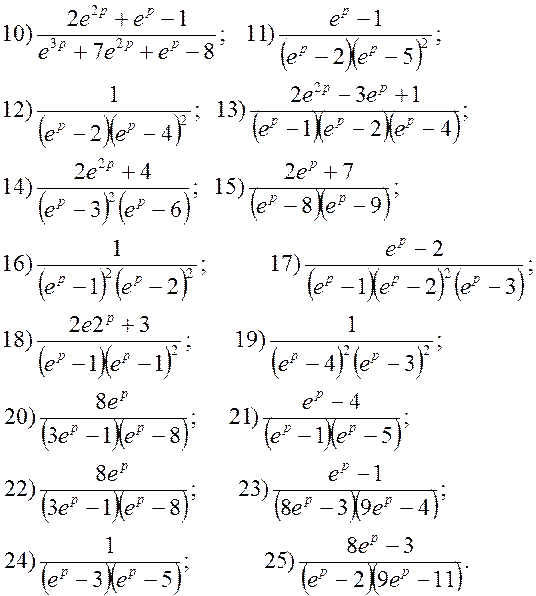
5. Знайти розв’язок лінійних рівнянь чи систем:
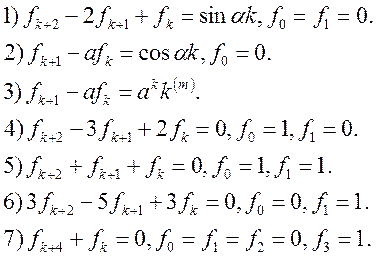
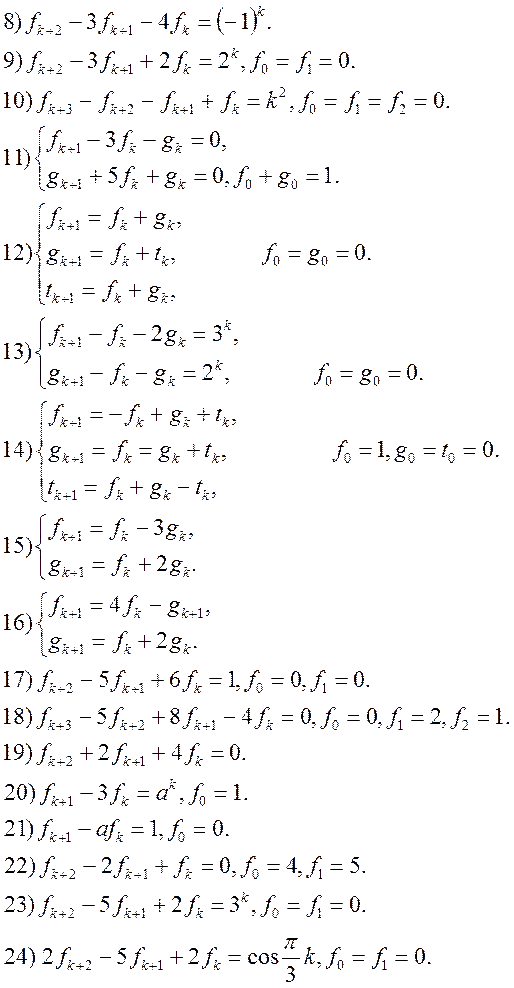
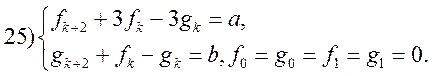
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.