Елементи теорії функцій комплексної змінної. Інтегральне перетворення Лапласа. Дискретне перетворення Лапласа, страница 9

        Вправи. Використовуючи теореми диференціювання і інтегрування зображень, знайти зображення функцій

               

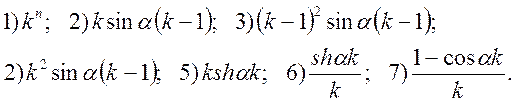
      3.6 Зображення скінчених різниць і суми оригіналів

        ТЕОРЕМА 1. Якщо то

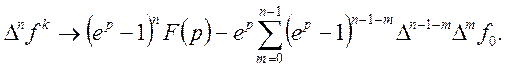
                (22)  

        Доведення. Відповідно до означення

         

        Застосовуючи до останньої формули теореми лінійності і випередження будемо мати

або

                                                      (23)

        Для скінченої різниці другого порядку одержимо

        Скориставшись теоремою випередження

        Остаточно маємо

                               (24) 

        Загальну формулу (22) можна довести на основі формул (23), (24) методом математичної індукції.

        Теорему доведемо.

        Означення. Сумою решіткової функції  називається решіткова функція

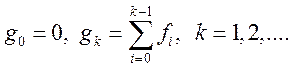                                                 (25)

        З приведеного означення випливає, що  тобто операція знаходження скінченої різниці першого порядку і операція знаходження суми решіткових функцій є взаємно обернені операції.

        ТЕОРЕМА 2. Якщо  то

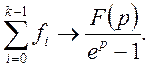                                                                     (26)

        Доведення. Хай  Відповідно до формули (23), ураховуючи рівність одержимо

        Звідси

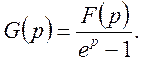
        Теорему доведено.

        Приклад. Знайти суму ряду

        Маємо 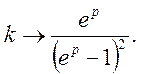Відповідно до формул (26), (20):

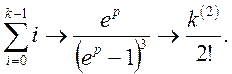
або

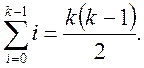
        Замінивши в останній формулі k – 1 на k остаточно одержимо

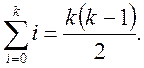
        Вправи. Знайти суми:

       

      3.7 Теореми про множення зображень та оригіналів

        Означення. Згорткою решіткових функцій  називають решіткову функцію

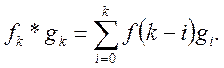                                                           (27)

        Із означення згортки випливає, що вона комутативна, тобто

        ТЕОРЕМА 1. добутку зображень відповідає згортка оригіналів, тобто

                                                             (28)

        Доведення. Відповідно до означення

        Помножимо останню рівність на

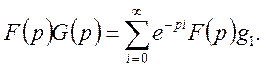
        Використовуючи теорему запізнення  і теорему лінійності 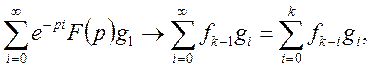 так як при

        Теорему доведено.

        Означення. Згорткою функції F(p) і G(p) називають функцію

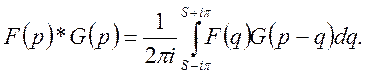                                      (29)

Якщо функція F(p) і G(p) аналітичні у півплощині  то згортка – аналітична функція у півплощині  Якщо перейти до змінних z і ξ по формулі  то отримаємо згортку функцій  для перетворення Лорана

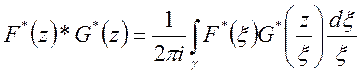                                       (30)

де γ – коло із області визначення функції .

        ТЕОРЕМА 2. Якщо  то

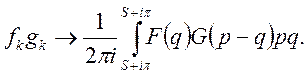                                               (31)

        Доведення. На основі теореми про лишки

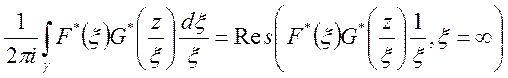
        Так як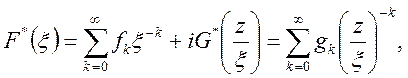

то

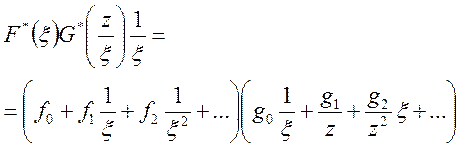
        В останній формулі коефіцієнт при  дорівнює лишку функції 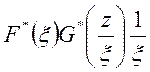 у точці .

        Маємо

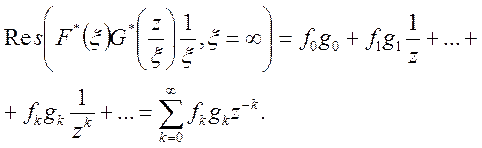
тобто    так як

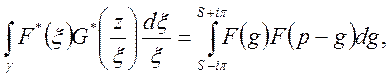
то

Теорему доведено.

        В и с н о в о к. Хай  тоді із формули (31) випливає

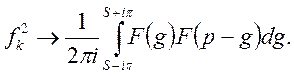
        Звідси при р=0

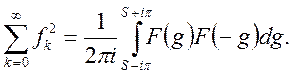
Вважаючи  будемо мати

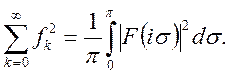                                                          (32)

        Формула (32) госит назву формули Парсеваля.

      3.8 Знаходження решіткової функції шляхом розкладання зображення на найпростіші дроби

Для знаходження функції  по відомому зображенню F(p) не обов’язково застосовувати формули (13), (14). Решіткову функцію  можна знайти безпосередньо, розкладаючи функцію F(p) на елементарні дроби виду

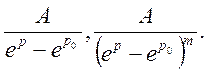
        Знайдемо оригінал для цих функцій. Маємо

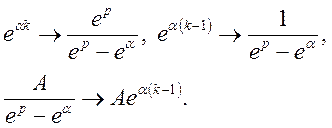
        Відомо

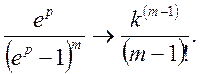
По теоремі зсунення

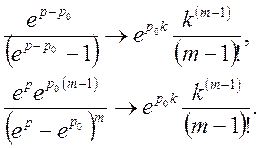
        По теоремі запізнення

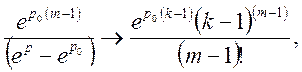
або

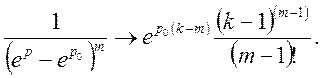
        Остаточно

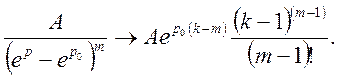                                          (34)

        Приклад. Знайти оригінал для функції F(p)

       

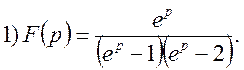
        Розглянемо функцію F(p) на елементарні дроби

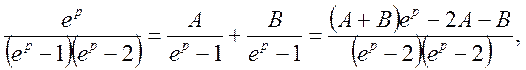
        Звідси

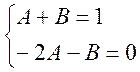
або

Застосуючи формули (23) маємо

       

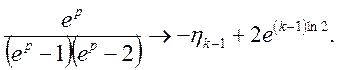
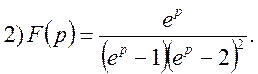
        Представимо функцію F(p) у вигляді суми елементарних дробів:

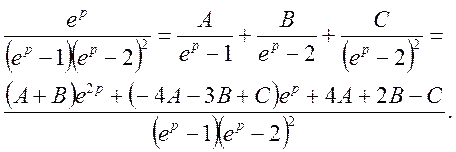
        Для невідомих постійних величин А, В, С одержимо систему

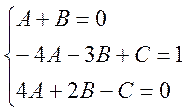
        Звідси А=1, В=-1, С=2.

        Таким чином, використовуючи формули (33), (34) будемо мати

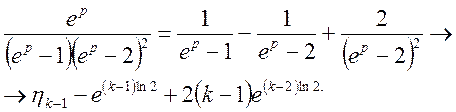
        Вправи. Знайти решіткові функції f_k, що відповідають зображенням F(p).

1)

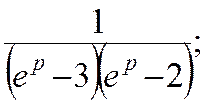
2)

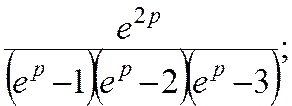
3)

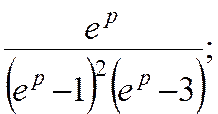
4)

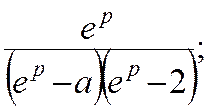
5)

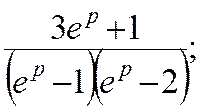
3.9 Формули відповідності для дискретного перетворення Лапласа

                                                      Таблиця 2

№

Оригінал fk

Зображення

1                                 

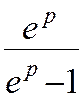
2.       k¹                                        

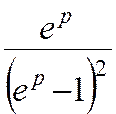
3         k²                                      

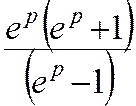
4         k³                                               

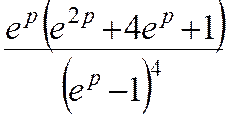
5         k⁴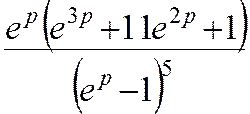                                             

6         k⁽²⁾ = k (k -1)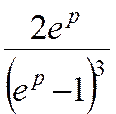                       

7         k ⁽ⁿ⁾ = k (k-1)…(k – n + 1)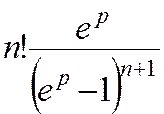       

8         e^αk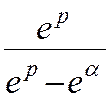                                         

9         ke^αk                                 

10        k²e^αk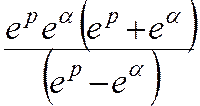                        

11        k⁽ⁿ⁾e^αk                                 

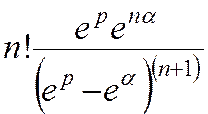
12        sinωk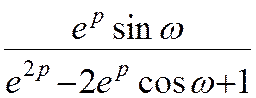                                     

13        cosωk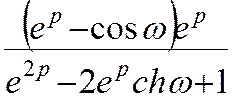                                  

14        shωk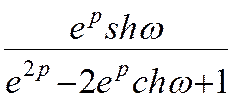                                     

15        chωk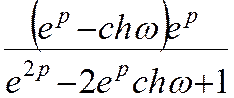                                                       

16        e^αk                                     

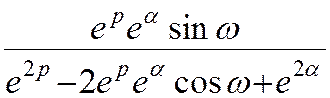
17        e^αk cosωk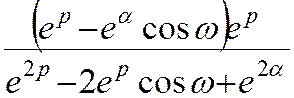                         

18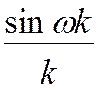                                         

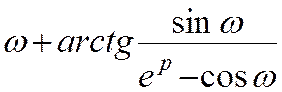
19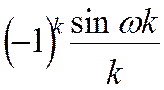                             

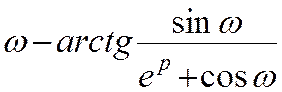
3.10 Різницеві рівняння

Означення.Лінійним різницевим рівняннямm-го порядку називається рівняння вигляду:

f_{k +m}+ a₁f_{k+m -1}+...+a_mf_k = g_k, a_m ≠ 0                (35)

Якщо g_k = 0, то рівняння (35) називається однорідним.

Нехай задані початкові умови f₀,f₁,...,f_{m - 1}.. Застосовуючи до обох частин рівняння (35) дискретне перетворення Лапласа і використовуючи теорему випередження, отримаємо рівняння відносно зображення F(p) функції f_k. Знайшовши з названого рівняння функцію F(p) і скориставшись формулами обернення чи їх аналогами, знайдемо невідому решіткову функцію f_k. Якщо початкові умови не задані, то вважаючи їх довільними постійними, отримаємо загальний розв’язок рівняння (35).