При цьому,
якщо ряд (7) збігається, решіткова функція ![]() називається
оригіналом, а функція
називається
оригіналом, а функція ![]() - зображенням. Відповідність
(7) позначається символом
- зображенням. Відповідність
(7) позначається символом ![]() або
або ![]() .
.
Якщо в
формулі (7) замінити ![]() , то будемо мати
, то будемо мати
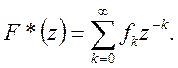 (8)
(8)
Формули (8) вводять z – перетворення решіткових функцій. Перетворення (8) відоме ще під назвою перетворення Лорана.
Розглянемо умови існування дискретного перетворення Лапласа.
ТЕОРЕМА.
Якщо решіткова функція ![]() задовольняє умовам
задовольняє умовам ![]() то її зображення
то її зображення ![]() існує в області
існує в області ![]() і є в цій області аналітичною
функцією.
і є в цій області аналітичною
функцією.
Доведення.
Маємо
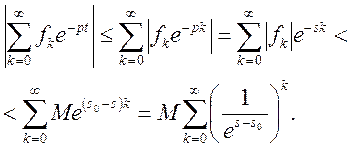
Останній
числовий ряд є сума членів геометричної прогресії із знаменником 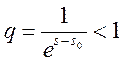 і значить, збігається при
і значить, збігається при ![]() Це означає, що ряд (7) збігається
рівномірно і його можна почленно диференціювати по р, тобто функція
Це означає, що ряд (7) збігається
рівномірно і його можна почленно диференціювати по р, тобто функція ![]() є аналітичною функцією при
є аналітичною функцією при ![]()
Теорему доведено.
Так як ![]() то
то ![]() Тобто
Тобто
![]() є періодичною функцією з періодом
є періодичною функцією з періодом ![]() . Таким чином, функція
. Таким чином, функція ![]() досить розглядати на півполосі
досить розглядати на півполосі ![]() (рис. 3).
(рис. 3).
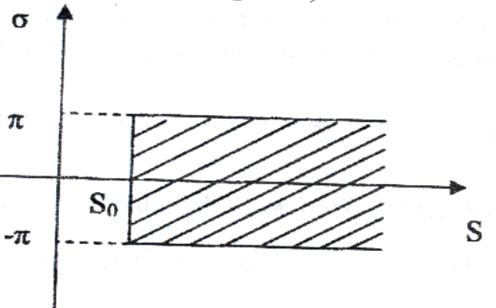
Рис. 3
Функція ![]() взаємно однозначно відображає
півполосу
взаємно однозначно відображає
півполосу ![]() на зовнішність кола радіуса
на зовнішність кола радіуса ![]() із розрізом вздовж відُ ємної частини дійсної вісі (рис. 4).
із розрізом вздовж відُ ємної частини дійсної вісі (рис. 4).
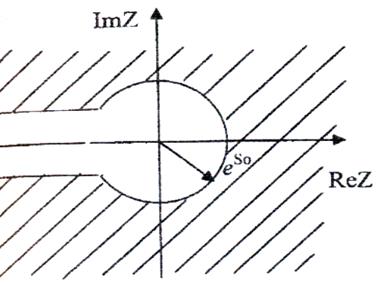
Рис.4.
Це значить,
що ![]() є однозначна аналітична функція в
області, показаній на рис. 4.
є однозначна аналітична функція в
області, показаній на рис. 4.
Приклад. Знайти зображення одиничної функції.
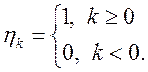
Маємо
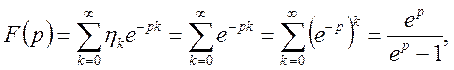
таким
чином, 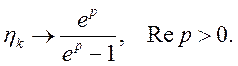
Вправи. Знайти зображення функцій
![]()
3.3 ОберненеD – перетворення Лапласа
Із теорії функції комплексної змінної відомо,
що коефіцієнти ![]() у формулі (8) знаходяться
по формулі
у формулі (8) знаходяться
по формулі
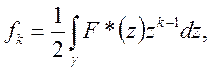 (9)
(9)
де γ – довільне коло з центром на початку координат належне області збіжності ряда (8).
Фактично
формула (9) задає обернене перетворення Лорана. Якщо в останній формулі перейти
від змінної z до змінної р по формулі ![]() то будемо мати
то будемо мати
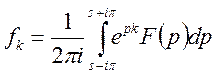 (10)
(10)
Формула (10) визначає обернене дискретне перетворення Лапласа. Використовуючи формулу про лишок при обчисленні інтегралів (9), (10) одержимо
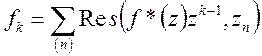 (11)
(11)
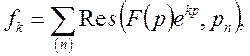 (12)
(12)
де ![]() - полюси функції
- полюси функції ![]()
Якщо функція ![]() має прості полюси, то формула (11)
приймає вигляд
має прості полюси, то формула (11)
приймає вигляд
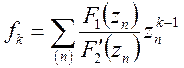 ,
,
а у випадку, коли кратність
полюса дорівнює ![]() , маємо
, маємо
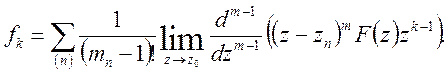 (14)
(14)
Формули (13) і (14) носять назву формул розкладення.
Приклад 1. Знайти оригінал функції
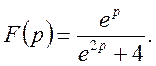
Маємо 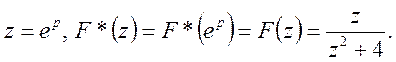
Функція ![]() має прості полюси
має прості полюси ![]() Відповідно до формул (13):
Відповідно до формул (13):
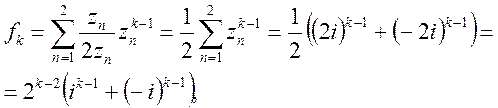
![]()
або 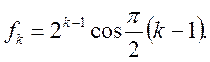
Приклад 2. Знайти оригінал функції
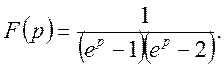
Маємо 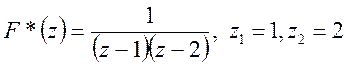 - прості полюси функції
- прості полюси функції ![]() .
.
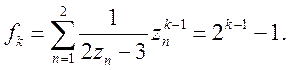
Розв’язок
останнього прикладу можна одержати безпосередньо, знаходячи ряд Лорана для
функції ![]() при
при ![]()
Представимо
функцію ![]() так:
так:
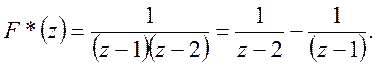
Використовуючи формулу для суми членів геометричної прогресії будемо мати
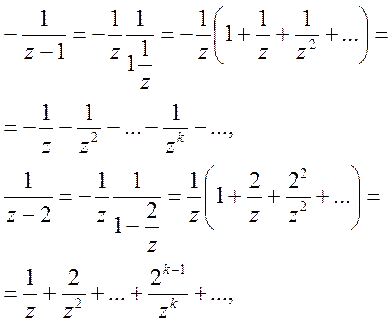
або 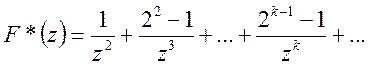
Таким чином, відповідно до формули (8)
![]()
Вправи.
1. Знайти
оригінал для функції ![]() , використовуючи формули
розкладання
, використовуючи формули
розкладання
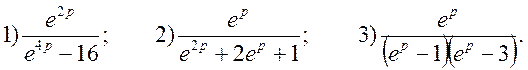
2. Знайти
оригінал функції ![]() за допомогою формул
розкладання, а також безпосередньо, знаходячи зображення
за допомогою формул
розкладання, а також безпосередньо, знаходячи зображення ![]() рядом Лорана
рядом Лорана
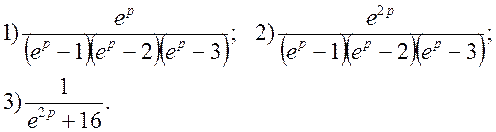
3.4 Основні властивості D-перетворення Лапласа
ТЕОРЕМА 1(лінійність перетворення). Для довільних комплексних чисел ![]() має місце формула
має місце формула
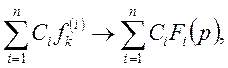 (15)
(15)
де ![]()
Доведення. Маємо
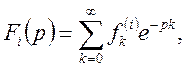
або 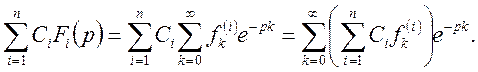
Теорему доведено.
Приклад 1. Знайти зображення решіткової функції
![]()
Відомо, що 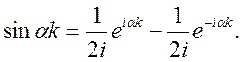
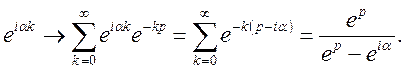
Застосовуючи теорему лінійності, будемо мати
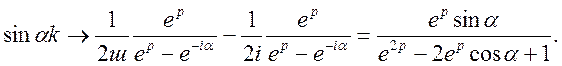
Остаточно 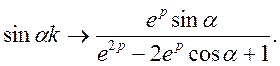
ТЕОРЕМА 2. (запізнення). Якщо n – натуральне число, то
![]() (16)
(16)
де ![]()
Доведення.
Решіткова функція ![]() при k<n.
при k<n.
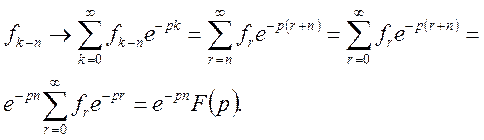
Таким чином, ![]()
Теорему доведено.
Приклад 2. Знайти зображення решіткової функції
![]()
Використовуючи результат прикладу 1 будемо мати
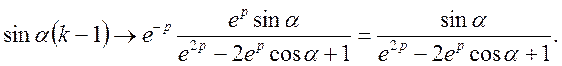
ТЕОРЕМА 3 (випередження). Для натурального n має місце формула
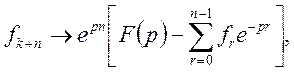 (17)
(17)
де ![]()
Доведення.
Позначимо ![]() . Будемо мати
. Будемо мати
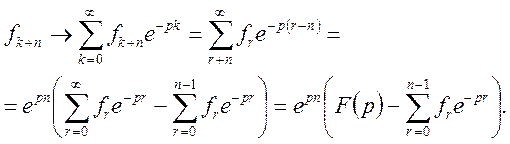
Теорема доведено.
Приклад 3.
Знайти зображення ![]()
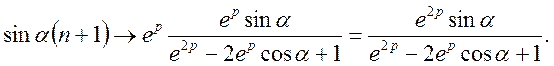
ТЕОРЕМА
4 (зсунення). Якщо ![]() довільне
комплексне число, то
довільне
комплексне число, то
![]() (18)
(18)
де ![]()
Доведення. Використовуючи означення перетворення Лапласа, маємо
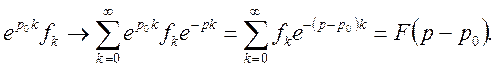
Теорему доведено.
Приклад 4.
Знайти ![]() для фунції
для фунції ![]() де
β – постійне число.
де
β – постійне число.
Відповідно до теореми 4 маємо
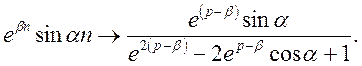
Вправи. Знайти зображення решіткових функцій ![]()
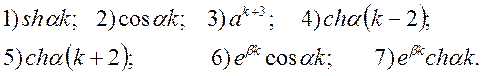
3.5 Теореми Диференціювання і інтегрування зображення
ТЕРЕМА 1 (диференціювання). Якщо ![]() то
то
![]() (19)
(19)
Доведення. Функція ![]() ,
що визначається рядом (7) є аналітична функція в області
,
що визначається рядом (7) є аналітична функція в області ![]()
![]()
Це значить, що ряд (7) можна почленно диференціювати
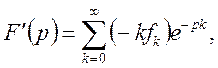
тобто ![]()
Продовжуючи цей процес, отримаємо формулу (19).
Теорему доведено.
Приклад 1.
Знайти зображення для узагальненої степеневої функції ![]()
Будемо мати
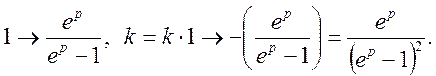
Далі по
теоремі запізнення 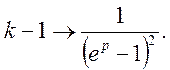 Застосовуючи до останньої
формули теорему диференціювання зображення, маємо
Застосовуючи до останньої
формули теорему диференціювання зображення, маємо
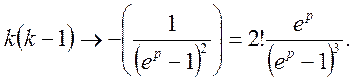
Продовжуючи далі, отримаємо
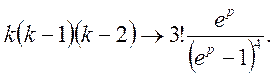
Методом математичної індукції можна отримати загальну формулу
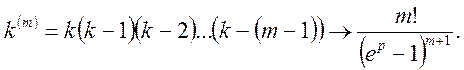 (20)
(20)
ТЕОРЕМА
2 (інтегрування). Якщо ![]() і
і 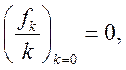 то
то
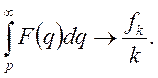 (21)
(21)
Доведення.
В силу аналітичності функції ![]() в ряді (7), можна
міняти порядок інтегрування і сумування. Маємо
в ряді (7), можна
міняти порядок інтегрування і сумування. Маємо
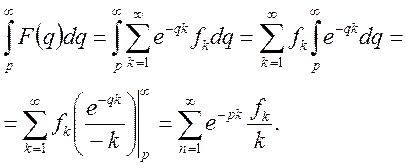
А це значить,
що 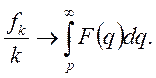
Теорему доведено.
Зауваження.
Якщо 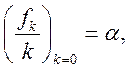 то
то
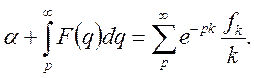
Приклад 2.
Знайти зображення для функції 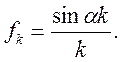
Маємо
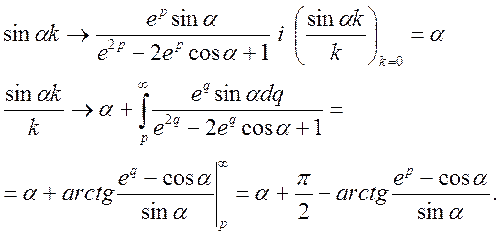
Остаточно
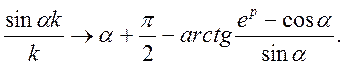
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.