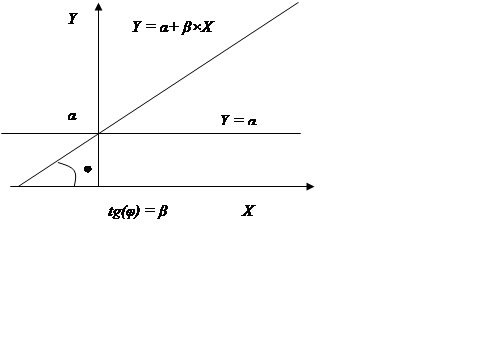
де α і β – невідомі параметри, геометричний зміст яких полягає в наступному. Параметр α визначає крапку перетинання прямої Y = α с віссю ординат, а другий – β – тангенс кута нахилу прямої (3.2) до осі абсцис (мал. 3.1);
експонентна
Y = α ×EXP(β×X); (3.3)
статечна
Y = α ×Xβ ; (3.4)
показова
Y = α × βX (3.5)
гіперболічна
Y = α + β/X (3.6)
поліноміальна
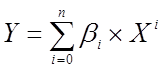 (3.7)
(3.7)
 де n > 1, і ін. Співвідношення (3.3)-(3.6) відповідними
перетвореннями можуть бути зведені до лінійної залежності типу (3.2). Для
зв'язку типу (3.7) це, узагалі говорячи, неможливо.
де n > 1, і ін. Співвідношення (3.3)-(3.6) відповідними
перетвореннями можуть бути зведені до лінійної залежності типу (3.2). Для
зв'язку типу (3.7) це, узагалі говорячи, неможливо.
Більшість традиційних економічних теорій містить відображення зв'язків між економічними категоріями у виді таблиць, чи графіків функціональних співвідношень.
 Виконання реальних економічних
вимірів показників X і Y завжди приводить до ситуації, що їхні
значення не можуть бути розташовані на деякій лінії типу (3.2)-(3.7). Тому
першого і другого припущень виявляється недостатньо для реалізації мети
дослідження, що складає в перебуванні адекватної форми залежності між
факторами Y і Y.
Виконання реальних економічних
вимірів показників X і Y завжди приводить до ситуації, що їхні
значення не можуть бути розташовані на деякій лінії типу (3.2)-(3.7). Тому
першого і другого припущень виявляється недостатньо для реалізації мети
дослідження, що складає в перебуванні адекватної форми залежності між
факторами Y і Y.
Один з можливих підходів складається у введенні припущення про наявність фактора стохастичности і введенні його в модель. Обговоримо можливі передумови його появи. Припустимо, що ми виконали виміри значень ознак X і Y у N економічних об'єктів і в результаті одержали N пару даних (Xi, Yi ), i = 1, 2, …, N...
Наші економічні об'єкти володіють цілим поруч інших ознак, наприклад, розміром, складом і т.д. Вважаємо, що об'єкти вже розділені на групи по обраних ознаках тим чи іншому способу. Аналізуємо деяку групу об'єктів (нехай вона містить перші n одиниць). В умовах гіпотези лінійності зв'язку між перемінними X і Y для даної групи економічних об'єктів можемо припустити, що група в цілому характеризується зв'язком виду
Y’ = α + β×X’,
де кожен представник групи має значення ознаки X, рівне X’ . Природно, що значення ознаки Y для них різні. Тому
Y’ = α + β×X’ + Ui, i =1, …, n,
де Ui – відхилення конкретного значення ознаки Yi від центрального, групового.
Може бути запропонований мінімум три шляхи раціонального пояснення включення в рівняння (3.2) стохастической добавки U:
Y = α + β×X + U. (3.8)
Перше розуміння полягає в тому, що в дійсності на результуючий фактор Y може впливати крім X цілий ряд інших факторів Z, U, V, W і т.д. Не усі вони можуть бути отслежены чи враховані кількісно. Вважаємо, що замість залежності виду
Y = f( Z, U, V, W , …),
де враховані менш важливі в порівнянні з X фактори Z, U, V, W ..., має місце рівняння
Y = f( X, U).
У ньому одного перемінна U призначена для
відображення сумарного ефекту факторів Z, U, V, W у впливі на Y.
При цьому ефект може бути як позитивним, так і негативним. Якщо виявиться, що
малі значення зустрічаються частіше чим великі, то про U можна говорити
як про випадковій перемінній з нульовим математичним чеканням і кінцевою
дисперсією ![]() Через те, що число явне неврахованих
факторів значно, а їхній можна вважати незалежними, залучення центральної
граничної теореми дозволяє трактувати випадкову величину U нормально
розподіленої.
Через те, що число явне неврахованих
факторів значно, а їхній можна вважати незалежними, залучення центральної
граничної теореми дозволяє трактувати випадкову величину U нормально
розподіленої.
Друге трактування наявності випадкового фактора в рівнянні (3.8) полягають у тому, що економічні об'єкти функціонують за участю людей, вплив яких на результати діяльності детерминировано пророчити не можна. Точно так само апріорі немає ніяких підстав затверджувати, що вид функціональної залежності обраний правильно.
Третє трактування присутності фактора випадковості U у рівнянні (3.8) зв'язана з помилками, що виникають у результаті виконання спостережень і вимірів.
Більш того, помилки, зв'язані з вибором виду рівняння, можуть накладатися, причому не обов'язково аддитивно, у виді додаткового доданка.
Таким чином, детальний аналіз суті специфікації форми зв'язку між перемінними X і Y (припущення 2) привів до необхідності висування ряду гіпотез про властивості розподілу імовірностей для випадкового збурювання U. Гіпотези відносяться до математичного чекання, дисперсії і ковариациям і складаються в найпростішому випадку в наступному:
а)
Yi = α + β×Xi + Ui, i =1, …, n, (3...9)
б)
M(Ui) = 0; (3.10)
 (3.11)
(3.11)
У співвідношеннях (3.9) і (3.11) параметри α, β,
![]() вважаються невідомими, а
вважаються невідомими, а ![]() – постійної. На основі спостережень
над X і Y необхідно не тільки статистично оцінити зазначені
параметри (цим займається статистика), але і перевірити стосовно них деякі
гіпотези, а саме:
– постійної. На основі спостережень
над X і Y необхідно не тільки статистично оцінити зазначені
параметри (цим займається статистика), але і перевірити стосовно них деякі
гіпотези, а саме:
- чи дійсно, що α = 0?
- с якою вірогідністю можна затверджувати, що β = β0, де β0 – задана величина?
- чи є адекватної лінійна залежність між перемінними X і Y?
- на скількох оправданно тверджень про
сталість дисперсії ![]() ?
?
У теорії статистики існують стандартні методи, що дозволяють відповісти на поставлені питання. Эконометрическая теорія розвиває нові методи одержання статистичних висновків щодо економічних моделей і їх складових у тих випадках, коли стандартні методи незастосовні.
Одержимо оцінки параметрів α і β рівняння лінійної регресії (3.2) методом найменших квадратів і досліджуємо властивості цих оцінок.
У залежності від вихідних припущень щодо ознак X і Y, а також їхніх характеристик задачі одержання статистичних висновків можуть трактуватися по-різному.
Нехай спочатку виконуються перше і друге припущення, а також умови (3.9)-(3.11). Рівняння (3.2) запишемо для шуканих оцінок у виді
![]() ,
(3.12)
,
(3.12)
де ![]() – оцінки невідомих
параметрів
– оцінки невідомих
параметрів ![]() і
і ![]() ,
, ![]() – ордината прямої, що відповідає
даному значенню Х. Сукупність вибіркових значень ознак Х и Y
задамо векторами
– ордината прямої, що відповідає
даному значенню Х. Сукупність вибіркових значень ознак Х и Y
задамо векторами
![]()
де Т – знак транспонування.
Уведемо позначення,

Природно покласти ![]() . Нехай також
. Нехай також ![]() .
.
Уведемо, нарешті, величину
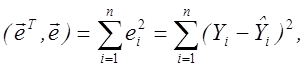 (3.13)
(3.13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.