Радиоавтоматика: Учебное пособие для практических занятий, страница 5

Определить установившуюся ошибку следящей системы при воздействиях: 1) x(t)=20+2tи 2) x(t)=20+2t–0,5t², если известна передаточная функция

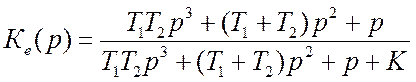            (18.1)

и заданы параметры: K=100 с^–1; T₁=0,1 c; T₂=0,01 c.

Решение

Передаточную функцию K_e(p) преобразуем к виду

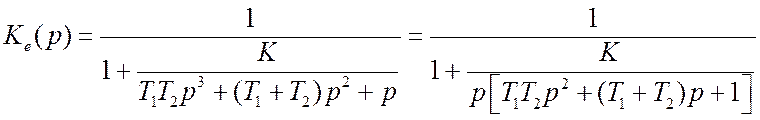. (18.2)

Отсюда находим передаточную функцию разомкнутой системы

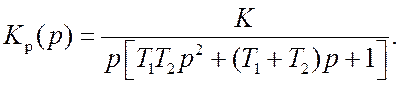                         (18.3)

 Рассматриваемая система имеет первый порядок астатизма и добротность K₁=K=100 с^–1. Следовательно, установившаяся динамическая ошибка в первом случае равна

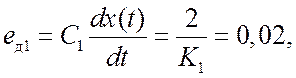
а во втором случае

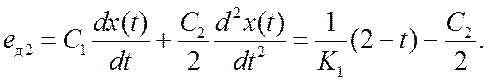
Для нахождения коэффициента С₂/2 используем уравнение (11.8) (лекция 11), которое в данном случае принимает вид

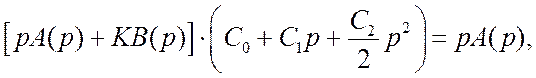             (18.4)

где A(p)=T₁T₂p²+(T₁+T₂)p+1, а B(p)=1.      

Приравнивая коэффициенты при p² в обеих частях уравнения, находим

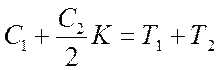
или

.

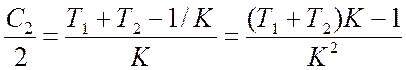Подставив значения параметров K, Т₁ и Т₂, получим С₂/2=0,001.

Окончательно для ошибки имеем

Первая составляющая (0,019) определяет скоростную ошибку, а вторая     (–0,01t) – ошибку по ускорению. Как видим, вклад составляющей – С₂/2=–0,001 действительно мал, и можно полагать, что .

Пример 19

Провести оптимизацию системы (рис. 19.1) по параметру k_и при воздействии  и помехе  – белом шуме с спектральной плотностью N₀ Bт /Гц.

Решение

Оптимизацию проводим в соответствии с критерием (1.106), так как воздействие детерминированное.

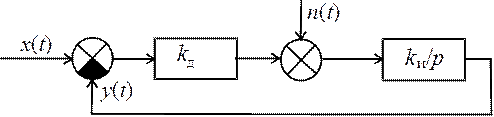
Рис. 19.1

Используя результаты п.п. 1.5.2, 1.5.3, для среднего квадрата ошибки (1.94) запишем

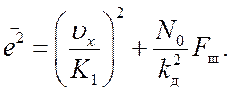                                      (19.1)

          Шумовая полоса системы в соответствии с (1.98) равна

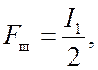
где

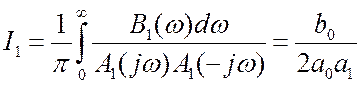                             (19.2)

– табличный интеграл вида (1.100), а полиномы

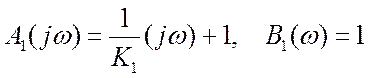
соответствуют передаточной функции замкнутой системы K_з(p)=1/[1+p(1/K₁)].

Подставив значения параметров a₀=1/K₁, a₁=1 и b₀=1 в (19.2), находим I₁=K₁/2.

          Шумовая полоса определяется добротностью системы по скорости K₁=k_дk_и:

                             (19.3)

Критерий оптимизации (1.106) в данном случае принимает вид

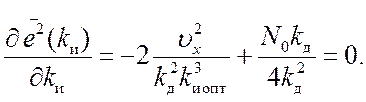                   (19.4)

Решая уравнение (19.4), получаем

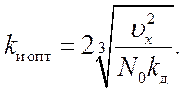
Оптимальное значение шумовой полосы и минимально достижимую ошибку находим подстановкой  в выражение для F_ш (19.3) и , (19.1):

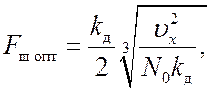                                         (19.5)

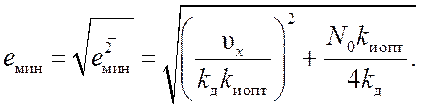
Анализ выражения (19.5) показывает, что оптимальное значение полосы системы определяется скоростью изменения воздействия  и интенсивностью шума N₀ (уменьшается с ростом N₀).     

Пример 20

Для системы, рассмотренной в примере 19, провести оптимизацию по параметру k_и при условия, что воздействие х(t) – стационарный случайный процесс с нулевым средним значением и спектральной плотностью

S_x(w)=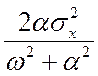

(помеха n(t), как и ранее, белый шум со спектральной плотностью N₀).

Решение

В качестве критерия оптимальности используем выражение (1.107), которое принимает вид

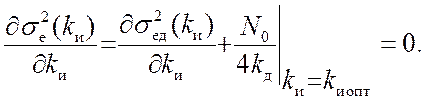                    (20.1)

Дисперсию динамической ошибки находим из (12.10) (лекция 12) после подстановки в него выражений для энергетического спектра воздействия и квадрата АЧХ

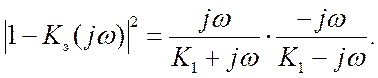
Используя для S_x(w) представление в виде

S_x(w) =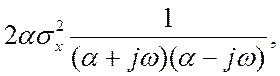

дисперсию динамической ошибки выражаем через табличный интеграл:

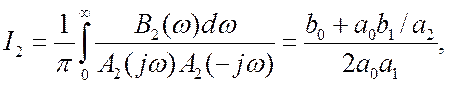           (20.2)

где полиномы

A₂(jw)=(jw)²+(a+K₁)(jw)+aK₁,

B₂(w)=w².

После подстановки параметров a₀=1, a₁=a+K₁, a₂=aK₁, b₀=1 и b₁=0 в выражение (20.2), получаем

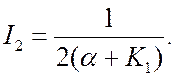
          Дисперсия динамической ошибки

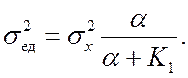
          С учетом этого выражения после решения уравнения (20.1) относительно параметра k_{и опт} имеем

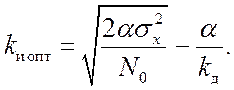                                      (20.3)

Значения оптимальной шумовой полосы и минимально достижимой ошибки находим подстановкой k _иопт в соответствующие выражения для F_{ш опт} и . Как видно из (20.3), значение k_иопт (а следовательно, F_шопт) определяется дисперсией  и шириной спектра a воздействия, а также интенсивностью шума N₀.  

Задача 40

Найти установившуюся ошибку в следящей системе (рис. 40.1), полагая, что воздействие х(t) = 20+2t–0,5t².

Рис. 40.1

Задача 41

Для системы с передаточной функцией

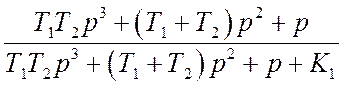
найти статическую ошибку, ошибку по скорости и ошибку по ускорению.

Задача 42

Для систем, ЛАХ которых представлены на рис. 42.1, а, б, в, г, найти установившуюся ошибку слежения при задающем воздействии x(t)=x₀+_xt+0,5_xt².

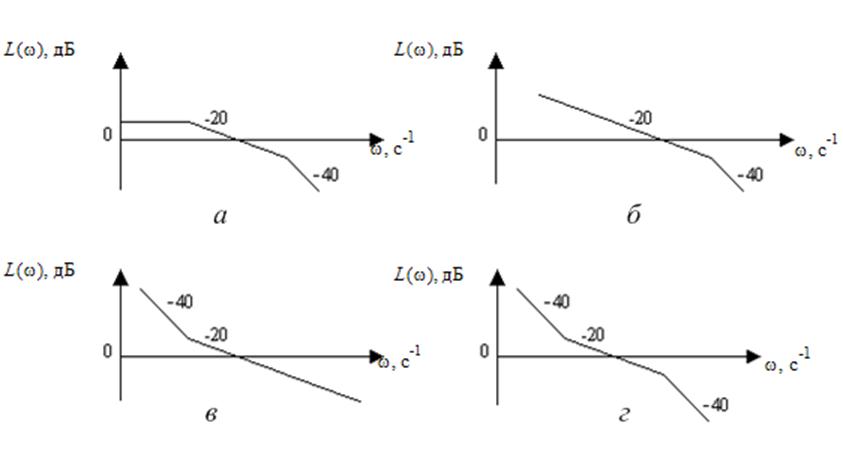
Рис. 42.1

Задача 43

Для замкнутой системы (рис. 43.1) найти шумовую полосу, а также установившуюся ошибку при задающем воздействии х(t) = 1+0,5t.

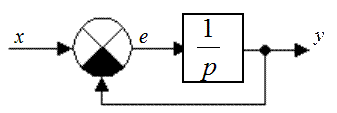
Рис. 43.1

Задача 44

Передаточная функция разомкнутой системы

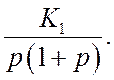
Найти шумовую полосу замкнутой системы при условии, что запас устойчивости по фазе Δφ = π/4 рад.

Задача 45

Передаточная функция разомкнутой системы

Найти шумовую полосу замкнутой системы при условии, что скоростная ошибка слежения е_ск < 0,01% от скорости изменения параметра х.

Задача 46

Для замкнутой системы (рис. 46.1) найти шумовую полосу, а также установившуюся ошибку при задающем воздействии х(t) = 20 – t.

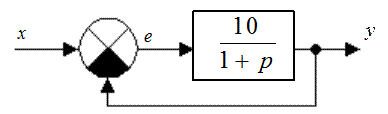
Рис. 46.1

Задача 47

Для замкнутой системы (рис. 47.1) определить значение параметра K₀, при котором обеспечивается заданная точность: дисперсия шумовой ошибки равна квадрату установившейся статической ошибки. Задающее воздействие х(t) = 10, а спектральная плотность белого шума N₀ = 0,1 Гц ^–1.

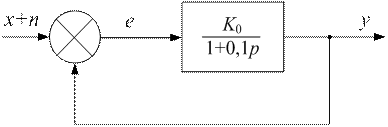
Рис. 47.1

Задача 48

ЛАХ разомкнутой системы имеет вид (рис. 48.1).

 

Рис. 48.1

Определить параметры системы, при которых шумовая полоса замкнутой системы равна 1Гц, а запас устойчивости по фазе Δφ > π/6 рад.

Задача 49

Провести оптимизацию системы (рис. 49.1) по параметру K, используя критерий минимума среднего квадрата ошибки. Воздействие х(t) = x₀, а помеха – белый шум с энергетическим спектром N₀ Гц ^–1.