Машиностроение \ Основы теории надежности и диагностики

Исследования и оценка параметров надежности и безотказности автомобилей: Лабораторные работы. Часть ІІІ (Примеры выполнения работ), страница 3

, т.е .

4.Тогда весь срок службы сопряжения найдем как сумму периодов приработки и нормальной эксплуатации:

 т.е.  

Рис. 3.1. График износа сопряжения

Выводы:

          1. Определен износ за время нормальной эксплуатации – δ2 =90мкм;

          2. Вычислен период нормальной эксплуатации - t2 =155,98 тыс. км;

          3. Определен период приработки – t1 = 3,12тчс. км;

          4. Определен  срок службы сопряжения – t = 159,1 тыс.км.

Лабораторная работа № 4.

Определение вероятности безотказной работы системы (резервирование)

Цель работы:

          Определить вероятность безотказной работы для системы, состоящей из  однотипных элементов с равными вероятностями безотказной работы, при последовательном и параллельном соединениях элементов.

Исходные данные (рис.4.1)

                   

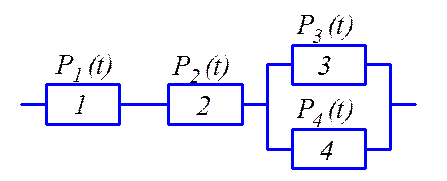
                                         Рис. 4.1. Система элементов.       

Дана система, состоящая из 4-х элементов, вероятность безотказной работы которых равна:

        

Определить вероятность безотказной работы системы.

Решение:

1. Для последовательно соединенных элементов 1-2, вероятность безотказной работы найдем, как произведение вероятностей этих элементов, т.е.

 .

2. Вероятность безотказной работы элементов, параллельно соединенных, 3-4 найдем по формуле:

.

3. Вероятность безотказной работы всей системы (вывод):

 .

Лабораторная работа № 5

          Определение средней наработки до отказа при известной вероятности безотказной работы.

Цель работы:

1 Найти среднюю наработку до отказа tср;

2 Определить:

-  плотность вероятности наступления отказов ;

-   вероятность отказа ;

-   интенсивность потока отказов ;

-  дисперсиюD;

-  среднее квадратичное отклонение ;

-   коэффициент вариации V.

Исходные данные:  , показатели безотказности подчиняются экспоненциальному закону.

Решение:

1. По формуле вероятности безотказной работы для экспоненциального закона

а средняя наработка до первого отказа  для этого закона равна

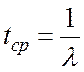
Тогда 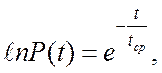 следовательно 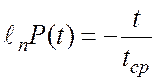, отсюда  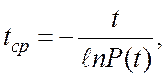т.е. .

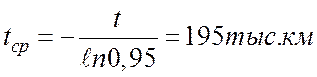2. Определим интенсивность отказов

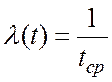, т.е.  .

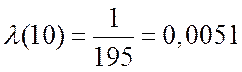3. Вычислим плотность вероятности отказа

     .

4. Вероятность наступления отказа

.

5. Дисперсия D:

по формуле для экспоненциального закона.

D=.

6. Среднее квадратичное отношение

т.е.  .

7. Коэффициент вариации V:

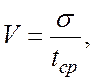   т.е.  .

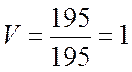Выводы:

1 Найдена средняя наработка до отказа tср;

2 Определены:

-  плотность вероятности наступления отказов ;

-   вероятность отказа ;

-   интенсивность потока отказов ;

-  дисперсияD;

-  среднее квадратичное отклонение ;

-   коэффициент вариации V.

 Результаты расчетов подтверждают соответствие заданному (экспоненциальному) закону.

Лабораторная работа  № 6

Определение вероятности безотказной работы при распределении отказов по нормальному закону (закону Гаусса)

Цель работы:

          Определить:

-  вероятность безотказной работы ;

-  плотность вероятности наступления отказов ;

-  вероятность отказа ;

-  интенсивность потока отказов ;

-   дисперсию D;

-   коэффициент вариации V.

-   

Исходные данные:     .

Решение:

1. Заменим переменную величину 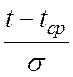  в формулах для нормального закона величиной  х, т.е. 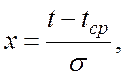 тогда в нашем случае :

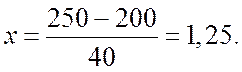
2. Из таблицы 2 приложения найдем значение  По формуле перехода от  нормированной функции  к вероятности отказа  

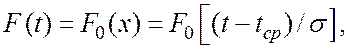  т.е.  .

       3. Тогда вероятность безотказной работы  определим из формулы:

т.е .

4.  По формуле перехода от центрированной функции  к исходной

Значение функции в таб. 3 приложения:

тогда

                                     .

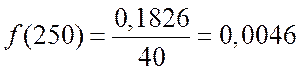5. Интенсивность отказов :

                                         .

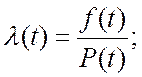
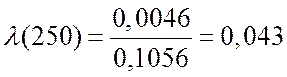6. Дисперсия равна квадрату среднего квадратичного отклонения, т.е.

.

7. Коэффициент вариации

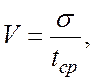 т.е. 

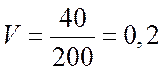
Выводы:

          Определены:

-  вероятность безотказной работы ;

-  плотность вероятности наступления отказов ;

-  вероятность отказа ;

-  интенсивность потока отказов ;

-   дисперсию D;

-   коэффициент вариации V.

Полученные расчетные величины подтверждают соответствие распределения ПН закону Гаусса.

Лабораторная работа №7

Определение наработки изделия по заданной вероятности отказа (безотказности)

Цель работы:

По заданной вероятности отказа (безотказной работы) найти:

-  наработку, соответствующую заданной вероятности ;

-   плотность вероятности наступления отказов ;

-  вероятность безотказной работы  (или вероятность отказа );

-   интенсивность отказов ;

-  дисперсию D;

-  коэффициент вариации V.

Исходные данные:

  ,      ,      

Решение:

1. Наработка  при заданной вероятности отказа определяется по формуле:

где индекс «»означает «вероятность», а - квантиль, т.е. применительно к  теории надежности, это наработка, при которой будет иметь место заданная вероятность отказа (или безотказной работы).

2. Функции  соответствует нормированная функция

при этом    и  .

Из таблицы 2 приложения найдем квантиль  при  (в таблице необходимо от заданной  найти значение х):

,  тогда .

3. Плотность вероятности наступления отказов  для нормального закона по формуле перехода от центрированной функции к исходной будет равна: 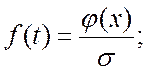 значение  определяется из таблицы 3 приложения:

тогда .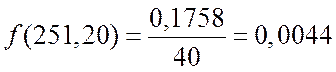

4. Вероятность безотказной работы

т.е.  .

5. Интенсивность отказов:   ,     .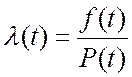

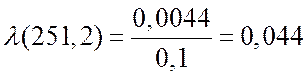6. Дисперсия

т.е.  .

7. Коэффициент вариации

.

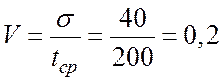Выводы:

По заданной вероятности отказа  определены:

-  наработка, соответствующая заданной вероятности ;

-   плотность вероятности наступления отказов ;

-  вероятность безотказной работы ;

-   интенсивность отказов ;

-  дисперсия D;

-  коэффициент вариации V.

Лабораторная работа № 8

Скачать файл