Моделирование. Математические схемы моделирования. Основные подходы к построению математической модели системы. Дискретно детерминированные системы (F-схемы), страница 9

В простейшем случае рассмотрим тело геометрически правильной формы с одномерным распространением тепла на отрезке от –R до R с симметрическими условиями на границах . Пренебрегая температурной зависимости мощности внутреннего тепло отделения, рассмотрим неравномерное распределение только по одной из пространственных координат.

Уравнение при нагреве неподвижного тела сводится к следующему уравнению теплопроводности:

.

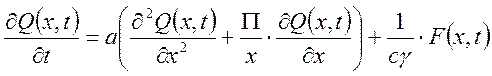С начальными условиями , .

И граничными условиями второго рода:

,    ,

,    ,

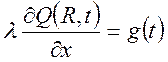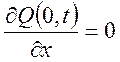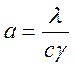                                                     - коэффициент температуры проводности.

 - коэффициент формы тела,

 - для бесконечной пластины толщенной ,

 - бесконечный цилиндр радиусом ,

 - шар, радиусом ,

 - удельная теплоемкость,

 - коэффициент теплообмена,

 - коэффициент теплопроводности.

В качестве выхода объекта выступает нестационарное температурное поле , а в роли внешних воздействий – удельная мощность внутреннего тепловидения , плотность теплового потока  на поверхности  и начальные распределения температур .

Каждый из этих воздействий может рассматриваться в качестве управления внутреннего или граничного неуправляемого внешнего фактора (возмущения).

Общее решение в соответствии с (21) на указанные входные воздействия при заданном температурном состоянии.

.

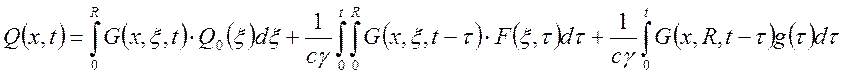Здесь функция Грина во втором двойном интеграле характеризует распределение температуры, возбуждаемый точечным источником тепла вида -функции сосредоточенной в момент времени  в точке .

Частными случаями функции Грина являются:

1. Функция Грина  характеризует распределение температуры возбуждаемая точечным источником тепла вида -функции, сосредоточенной в точке  в начальный момент времени .

2. Функция Грина  при .

Импульсная передаточная функция (функция Грина)  Является решением задачи,

,

,

,

,

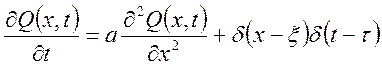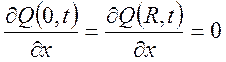при нулевых начальных и однородных граничных условиях.

Здесь используется разложение в бесконечный ряд Фурье по тригонометрической системе функции с зависящим от времени коэффициентами в виде экспоненты с отрицательными показателями степени быстровозрастающими по абсолютной величине.

.

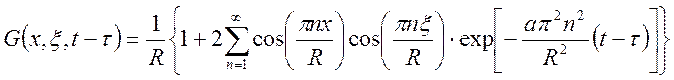Для одномерной задачи в общем случае (24*) стандартизирующая функция имеет вид:

,

где    -определяются из выражения вида:

,

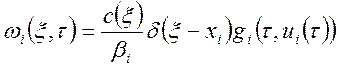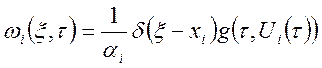,    при ,

,

, при  .

Для нашего случая:

,

,

,

,

,

,

,

,

.

Входное воздействие 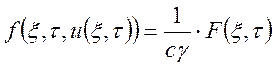, следовательно, стандартизирующая функция для нашей задачи запишется в виде:

.

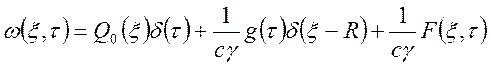Пусть плотность теплового потока на поверхности пластины  и начальное распределение температуры , тогда стандартизирующая функция упрощается до следующего вида:

.

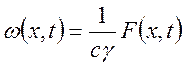Тогда решение рассматриваемой задачи описывается пространственно временной композицией вида:

.

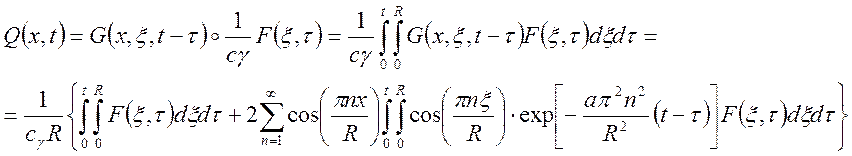Лекция № 13

Тепловые распределенные блоки

Типовой объект управления с распределенными параметрами с входным воздействием  и выходом , может аналогично объектами с распределенными параметрами рассматриваться в виде распределенного блока (черного ящика).

Отличие заключается в том, что входная и выходная величины, зависящие  не только от времени, но и от пространственных аргументов.

В общем случае объект с распределенными параметрами можно представить:

СРП:

 

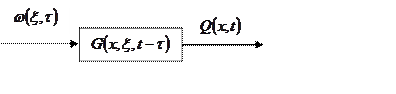ССП:

 

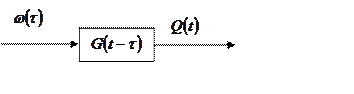Переходный х-блок

Представляет собой распределенный блок с сосредоточенным входным сигналом и распределенным выходным.

Это один из наиболее распространенных на практике вариантов для которого  стандартизирующая функция.

То есть рассматривается объект с сосредоточенным внешним воздействием  и фиксированным законом  пространственного распределения входного сигнала.

Тогда в соотношении, связывающим вход объекта с управлением  вынесем управляющее воздействие за знак пространственного интеграла:

,

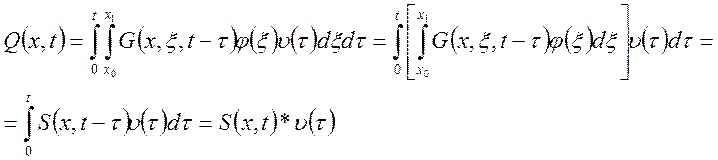где  * - операция свертки,

,

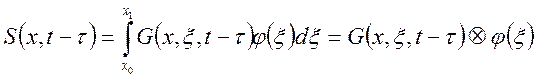 - пространственная композиция.

а) Х-блок с сосредоточенным внутренним управлением.

Пусть для системы (24*) выполняется следующее условие:

,

,

,

.

То есть рассматривается случай с входным воздействием только по сосредоточенному внутреннему управлению  с  фиксированным законом .

Следовательно, стандартизирующая функция имеет вид:

,

.

 

б) Х-блок с сосредоточенным граничным управлением в условиях второй и третьей краевой задачи.

Пусть в системе (24*) удовлетворяет следующее условие:

,

,

,

,

 или .

То есть рассматривая случай распределенного блока с граничным управлением , сосредоточенном в точке  на одной из границы области  определение пространственной переменной, при отсутствии других входных воздействий.

,

,

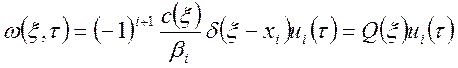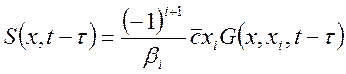Здесь

,

.

 

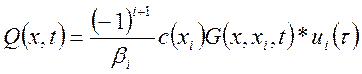в) Х-блок с сосредоточенным граничным управлением в условиях первой краевой задачи.

Пусть , тогда

,

,

,

,

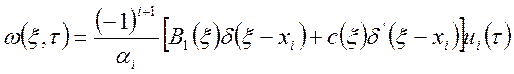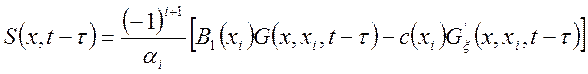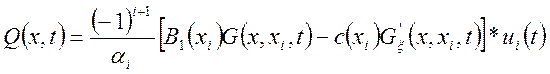где     .

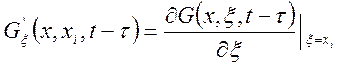Пример х-блока.

Рассмотрим нагрев пластины в условиях .

.

Стандартизирующая функция ,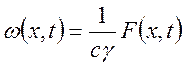

где  - мощность источников тепла.

Выходная величина определяется следующим образом:

.

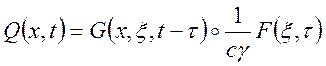Если  представить в виде произведения  и , где  - удельная величина источников тепла, выделяемого в нагретом теле,   - закон ее распределения по пространственной координате х-блок первоготипа.

Лекция № 14

Второй переходной -блок представляет собой блок с распределенным входным сигналом и сосредоточенным выходным.

В качестве последнего рассматривается значение функции состояния  в одной их  или  фиксированных  точках , где .

 

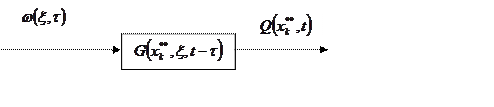Подобная ситуация может возникнуть, например, при формировании соответствующего сигнала обратной связи.

Третий тип. Переходный -блок – это распределенный блок с сосредоточенными входами и выходами, моделирует поведение функций состояния объекта  фиксированных точках  для  при сосредоточенном управлении .

Аналогично характеризуется объект с сосредоточенными параметрами, однако, -блок отличается от ОСП видом своей функции Грина.

Четвертый тип. Пространственное воздействие  при фиксированном характере  изменение входного сигнала во времени. Такие блоки не имеют аналогов в сосредоточенных системах.