Другие предметы \ Моделирование систем управления

Моделирование. Математические схемы моделирования. Основные подходы к построению математической модели системы. Дискретно детерминированные системы (F-схемы), страница 3

Теорема о дифференцируемости, оператор Лапласа:

,

.

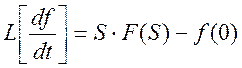Также уравнение можно записать в другом виде:

.

Так как мы находим передаточную функцию, то все наши начальные условия равны 0, тогда мы получаем уравнение:

.

Тогда передаточная функция окончательно записывается в виде:

.

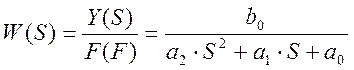Механические системы с линейным перемещением

Параметрами механических систем является масса демпфирования (трения) и упругость (эластичность).

Движение может происходить только в одном направлении.

 

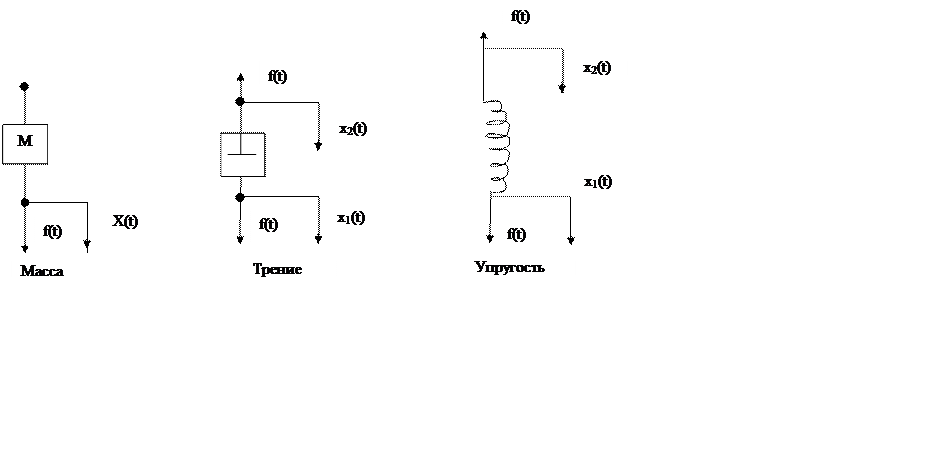
Сначала рассмотрим массу:

f(t) – приложенная сила,

х(t) – перемещение,

М – масса.

Все в соответствующих единицах измерения в соответствии со вторым законом Ньютона, можно записать следующее дифференциальное уравнение:

,

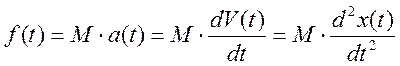где   - скорость;

 - ускорение.

Предполагается, что масса является жесткой, т.е. вероятная точка, с которой она соединена, не может перемещаться относительно нижней. Следовательно, положение верхней точки тоже равно x(t).

Для двух остальных механических элементов верхняя точка может перемещаться относительно нижней точки, следователь, для описания движения этих элементов потребуется две переменных.

Рассмотрим трение.

Математическая модель трения имеет уравнение:

,

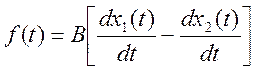где   В – коэффициент демпфирования.

Заметим, что сила трения прямо пропорциональна относительно скорости перемещения.

Уравнение движения для пружины определяется законом Гука:

,

где   K – модуль упругости.

То есть сила прямо пропорциональна разности положения концов пружины.

Приведенные уравнения справедливы для сил и перемещения, направления которых обозначено на рисунке стрелками.

Если какое-либо из направлений меняется на обратное, то в уравнениях нужно изменить знак соответствующего члена. Кроме того, полагают, что элементы трения и упругости имеют нулевую массу.

В основе уравнений движения этих механических элементов лежит закон Ньютона.

Рассмотрим простую механическую систему, изображенную на рисунке.

 


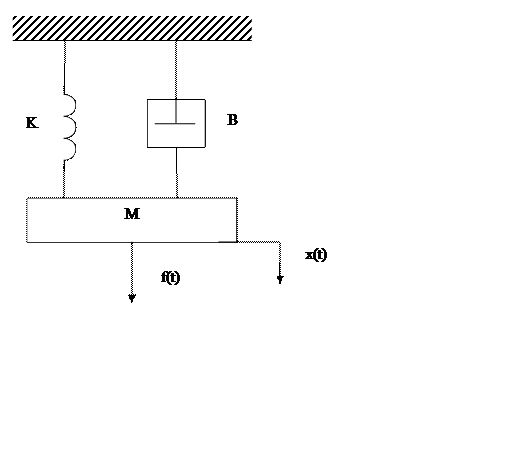По-прежнему предполагаем, что движение происходит только в одном направлении, как указано стрелкой.

На тело массой М действует три силы: внешняя сила, сила трения и упругая сила, следовательно, можно записать уравнение (*):

                                          .                                               (*)

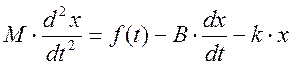Для данной системы передаточная функция должна связывать приложенную силу F(t) и положение массы x(t).

Преобразование по Лапласу уравнения (*), имеет вид (**):

                           (**)

Поскольку мы определяем передаточную функцию, то начальные условия полагаем нулевыми, таким образом, передаточная функция равна:

.

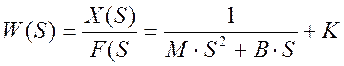Лекция № 4

Дискретно детерминированные системы (F-схемы)

В основе этого подхода лежит теория автомата.

Система представляется в виде автомата непрерывной дискретной информации и имеющего свое внутреннее состояние лишь в допустимые моменты времени.

Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы, снимаются выходные и которое может иметь некоторое внутреннее состояние.

Конечным автоматом, называется автомат, у которого множество состояний и входных сигналов, а, следовательно, и множество выходных сигналов является конечными множеством.

Абстрактно конечный автомат (от слова финити - автомат), отсюда название F-схема, характеризуется смесью элементов:

1. Конечным множеством входных сигналов х.

2. Конечным множеством выходных сигналов у.

3. Конечным множеством внутренних состояний – внутренний алфавит Z.

4. Начальными состояниями Z0, при чем .

5. Функции переходов .

6. Функция выходов .

Таким образом, F-схема задается следующим выражением:

.

Работа конечного автомата происходит по следующей схеме: в каждом такте t на вход автомата, находящегося в состоянии Z(t), подается некоторый сигнал X(t), на который он реагирует в такте (t+1) переходом в новое состояние Z(t+1) и выдачи некоторого выходного сигнала.

Для автомата первого рода, называемого также автоматом Миля, можно записать:

Автомат Миля.

,       

                                             ,          

Автомат Мура.

,   

,  

Для автомата Мура функции не зависят от входной переменной x(t).

По числу состояний различают конечные автоматы с памятью и без памяти.

Автоматы с памятью имеют более одного состояния, а автоматы без памяти (например, логические схемы) обладают лишь одним состоянием.

При этом его работа заключается в том, что ставится в соответствие каждому x(t) определенный выходной сигнал y(t), т.е. для автомата без памяти, функция выхода записывается:

,         

По характеру отчета дискретного времени конечные автоматы делятся на синхронные и асинхронные.

В синхронных F автоматах в моменты времени, которые автомат считывает, входные сигналы определяются принудительно с синхросигналами (синхронные RS-триггеры).

 Асинхронный F автомат считывает входной сигнал непрерывно и поэтому реагирует на достаточно длинный входной сигнал постоянной величины x, он может несколько раз изменять состояние, пока не перейдет в устойчивое, которое уже не может быть изменено данным выходным сигналом.

Способы задания автоматов

Существует несколько способов задания F автоматов, но наиболее часто используется табличный, графический и матричный способы.

Табличный способ основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы – его состояние.

Пример автомата Мили.

Xi

ZK

Z0

Z1

Z2

…

ZK

 

Переходы Z(t+1)

X1

φ(Z0, X1)

φ(Z1, X1)

φ(Z2, X1)

…

X2

φ(Z0, X2)

φ(Z1, X2)

φ(Z2, X2)

…

.

.

.

 

Выходы

X1

Ψ(Z0, X1)

Ψ(Z1, X1)

Ψ(Z2, X1)

…

X2

Ψ(Z0, X2)

Ψ(Z1, X2)

Ψ(Z2, X2)

…

.

.

.
Скачать файл