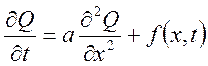
![]()
![]() (9)
(9)
Уравнение (9) – неоднородное уравнение теплопроводности, учитывающее внешнее воздействие от внутренних источников вещества и энергии.
Включив в правой части уравнений (8) и (9)
дополнительный член ![]() , получим уравнение
теплопроводности в цилиндрической системе пространственных координат.
, получим уравнение
теплопроводности в цилиндрической системе пространственных координат.
Уравнения эклектического типа
В уравнениях этого типа отсутствует производная от ![]() по времени t и описывают стохастическое
состояние ОРП.
по времени t и описывают стохастическое
состояние ОРП.
1) Гельмгольца
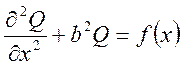
![]() (10)
(10)
2) Пуассона
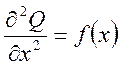
![]() (11)
(11)
при ![]() в уравнении (10)
в уравнении (10)
3) Лапласа (эллиптического типа)
При ![]()
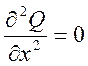
![]() (12)
(12)
Уравнения (11) и (12) моделируют в распространении температуры потенциала скоростей при стационарном течении несжимаемой жидкости потенциал электрического поля в задачах электрической статики и т.д. при отсутствии или наличии внешних воздействий соответственно.
Уравнение (10) описывает многие физические процессы теплопроводности, диффузии в движущихся средах, напряженности поля и т.д.
Замечание:
В общем случае описание функции не сводится к перечисленным уравнениям так как:
- оператор L может быть нелинейным;
- уравнения могут быть многополярными (в двух или трех мерных пространственных координатах);
- порядок уравнения может быть больше второго;
- поведение СРП может моделироваться не одним, а системой уравнений в частных производных, т.е. описываться векторным уравнением.
Общая характеристика условия однозначности
Начальные условия
Начальная функция ![]() в
уравнении (2) должна задавать начальные (при
в
уравнении (2) должна задавать начальные (при ![]() )
распределения во всей замкнутой области
)
распределения во всей замкнутой области ![]() самой
функции состояния
самой
функции состояния ![]() и
и ![]() производных
по времени t, где
производных
по времени t, где ![]() - порядок старшей
производной в уравнении (1).
- порядок старшей
производной в уравнении (1).
![]()
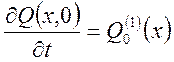
![]() (13)
(13)
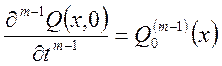
![]()
где
![]()
в уравнении (2).
Для гиперболических уравнений (5) – (7) должны быть
заданы ![]() равное:
равное:
![]()
![]()
Для параболических уравнений (8) – (9):
![]()
![]()
Для электрических уравнений (10) – (12) начальные условия отсутствуют так как там нет производных по времени.
Граничные условия
При исследовании процессов в неограниченном пространстве (простейший случай) граничные условия отсутствуют.
При ограниченном объеме области ![]() линейный оператор Г в уравнении (3)
может иметь один из следующих видов:
линейный оператор Г в уравнении (3)
может иметь один из следующих видов:
1) Граничные условия первого рода (первая краевая задача) – Дирихле.
![]()
![]()
![]() (14)
(14)
То есть должна быть задана сама функция состояния на
границе ![]() .
.
2) Граничные условия второго порядка (вторая краевая задача) – Нейман.
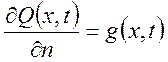
![]()
![]() (15)
(15)
Задается граничная функция состояния на границе пространственной области.
3) Граничные условия третьего рода (третья краевая задача, смешанная задача).
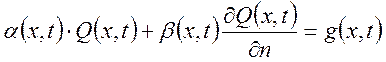
![]()
![]() (16)
(16)
где
![]() и
и ![]() -
заданные функции на границе
-
заданные функции на границе ![]() , принимающие в
частности постоянные значения.
, принимающие в
частности постоянные значения.
В общих случаях возможно следующее:
1. На различных участках границы ![]() могут задаваться граничные условия
различного типа.
могут задаваться граничные условия
различного типа.
2. Для объектов с уравнением первого порядка всегда рассматривается первая краевая задача.
3. Граничные условия значительно упрощаются для
области ![]() правильной формы.
правильной формы.
Лекция № 9
Импульсные переходные функции и основные соотношения вход-выход
Рассмотрим СРП, функция соотношение, которого описывается уравнением (4).
После приведенные к конечной форме записи (не содержащие смешанных производных), это уравнение имеет вид:
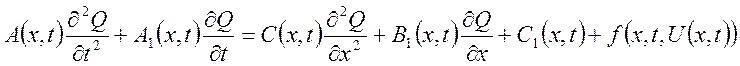 (17)
(17)
![]()
![]()
Это уравнение имеет вид (17) с типовыми начальными условиями, которые преобразуют в рассматриваемом одномерном случае, вид:
![]()
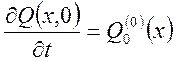 (18)
(18)
![]()
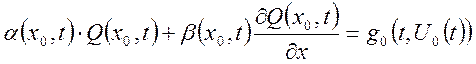 ,
,
![]() (19)
(19)
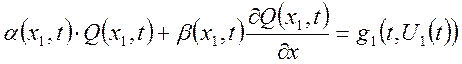 ,
, ![]() (20)
(20)
где
![]() - входные воздействия, которые в
общем случае могут включать внутреннее управление
- входные воздействия, которые в
общем случае могут включать внутреннее управление ![]() ,
, ![]() и
и ![]() ,
реализуемые за счет внутренних источников энергии или вещества.
,
реализуемые за счет внутренних источников энергии или вещества.
Пример:
Индукционный нагрев металлических изделий, в процессе которого внутренние источники тепла возбуждают электромагнитным полем индуктора на основе эффекта ветровых токов.
Основное соотношение, связывающее выход объекта при заданном начальном состоянии с выходными воздействиями, определяется общим решением, представленном в следующей интегральной форме:
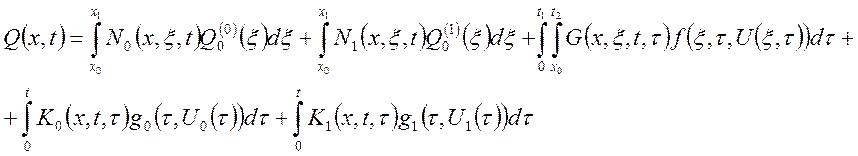 (21)
(21)
![]()
где
![]() и
и ![]() -
переменные интегральные по пространственной координате и времени соответственно.
-
переменные интегральные по пространственной координате и времени соответственно.
Первый и второй интегралы по пространственной
координате определяется соответствующей общему решению, соответствующего
влияния ![]() , начальных распределений
, начальных распределений ![]() и
и ![]() .
.
Четвертый и пятый интегралы по времени учитывают
сосредоточение входные воздействия ![]() и
и ![]() (19)-(20) по граничным условиям.
(19)-(20) по граничным условиям.
Третий двойной интеграл по пространственно временной
области изменения пространственно ![]() и временного
и временного ![]() аргумента распределенного входного
воздействия
аргумента распределенного входного
воздействия ![]() и отражает его вклад в реакцию
объекта.
и отражает его вклад в реакцию
объекта.
![]() - ядра линейных
интегральных операторов.
- ядра линейных
интегральных операторов.
В частности ![]() в третьем
интеграле есть функция Грина.
в третьем
интеграле есть функция Грина.
Функция Грина
Если в краевой задаче (17)-(20) начальные условия нулевые, а граничные условия однородные, т.е.
![]()
![]()
![]()
![]()
и
функции ![]() в уравнении (17) представляется как
в уравнении (17) представляется как
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.