Анализ и синтез механизмов сенного пресса (Силовой анализ)

Определение уравновешивающего момента и реакции в кинематической паре О

Составляем уравнения равновесия начального звена механизма (рис. 5.3):

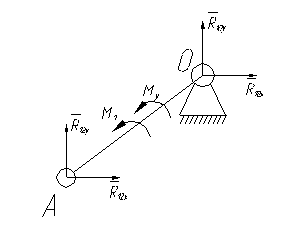Рис. 5.3. Силовой анализ начального звена

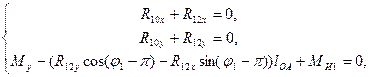                                   (5.2)

где , , ,  – проекции на оси координат реакции на звено 1 стойки 0;  – уравновешивающий момент.

Решая (5.2), найдем:

5.3. Определение уравновешивающего момента и реакций

в кинематических парах графическим методом

5.3.1 Силовой анализ структурной группы 4 – 5

Рисуем структурную группу 4 – 5 и прикладываем к ней все действующие силы и моменты. Реакцию  изображаем разложенной на нормальную  и касательную  составляющие.

Силовой анализ группы начинаем с определения касательной составляющей реакции, для чего составляем уравнение моментов относительно точки D для звена 4:

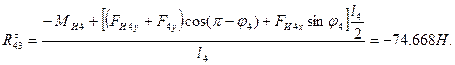
Запишем векторное уравнение сил, действующих на эту группу в целом, таким образом, чтобы неизвестные реакции находились по краям:

                     (5.3)

Уравнение (5.3) решаем графическим методом построения планов сил. Выбираем масштабный коэффициент сил . Находим для известных сил величины отрезков, которыми они изображаются на плане сил:

Последовательно, начиная с ab, откладываем на плане сил векторы, изображающие силы. Через точку a проводим линию действия реакции  перпендикулярную , а через точку g – реакции . Точка k пересечения этих линий определит отрезки kb и kg, которые изображают искомые реакции. Истинные величины реакций находим следующим образом:

Найдем теперь точку приложения реакции . Для этого найдем сумму моментов относительно точки D для звена 5:

откуда

.

Данные, полученные в результате расчетов графическим и аналитическим методом, приведены в табл. 5.2.

Таблица 5.2

Результаты силового анализа структурной группы 4 – 5

5.3.2 Силовой анализ структурной группы 2 – 3

Рисуем структурную группу 2 – 3 и прикладываем к ней все действующие силы и моменты. Реакцию  изображаем разложенной на нормальную  и касательную  составляющие.

Силовой анализ группы начинаем с определения касательной составляющей реакции , для чего составляем уравнение моментов относительно точки А для звеньев 2 и 3:

Длины плеч берем из плана положений механизма. Решив последнее уравнение, найдем:

Составляем векторное уравнение сил, действующих на группу 2 – 3 в целом. Уравнение записываем таким образом, чтобы неизвестные величины находились по краям:

Выбираем масштабный коэффициент сил . Находим для известных сил величины отрезков, которыми они изображаются на плане сил:

Последовательно, начиная с отрезка (ab), откладываем остальные отрезки в соответствии с векторным уравнением сил. Через точки a и е плана сил проводим линии действия неизвестных составляющих  и . Точка f пересечения этих линий определяет отрезки (fa) и (fe), изображающие реакции  и . Истинное значение этих реакций определится:

;

.

Суммируя графически  и , находим полную реакцию :

.

Данные, полученные в результате расчетов графическим и аналитическим методом, приведены в табл. 5.3.

Таблица 5.3

Результаты силового анализа структурной группы 2 – 3

5.3.3 Силовой анализ начального звена

Прикладываем к начальному звену все силы и моменты. Здесь  – уравновешивающий момент, а .

Запишем уравнение суммы моментов относительно точки О:

откуда

Находим погрешности определения уравновешивающего момента :

5.3. Определение уравновешивающего момента

методом рычага Жуковского

Строим повернутый на 90⁰ план скоростей механизма, к которому в соответствующих точках прикладываем заданные силы и силы инерции, сохраняя их истинные направления (рис. 5.4).

Моменты инерции ,  и  заменяем парами сил   и  соответственно, которые прикладываем перпендикулярно отрезкам pa₁, pd, bc.

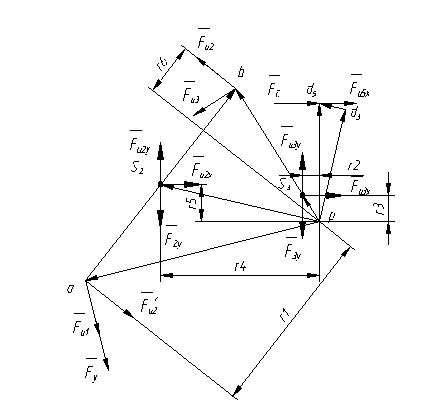Рис. 5.4. Рычаг Н.Е. Жуковского

Модули этих сил определятся:

Все силы переносим в одноименную точку плана скоростей без изменения ее направления. В точке а плана скоростей прикладываем неизвестную уравновешивающую силу .

Записываем уравнение моментов сил относительно полюса плана скоростей:

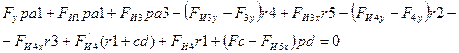              (5.4)

Решив (5.4) найдем силу :

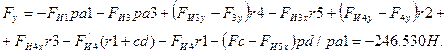
Зная величину , найдем уравновешивающий момент :

Отклонение найденного с помощью рычага Жуковского значения момента