Построение планов положений исследуемого механизма комбайна.
Выбираем масштабный
коэффициент длин 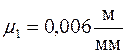 и
рассчитываем чертежные размеры звеньев (табл. 3.2).
и
рассчитываем чертежные размеры звеньев (табл. 3.2).
Чертежные размеры звеньев.
Т а б л и ц а 3.2.
|
AB, мм |
BC, мм |
CD, мм |
BE, мм |
EP, мм |
|
|
|
|
|
10 |
156,6 |
16,6 |
61,6 |
61,6 |
66,6 |
91,6 |
16,6 |
50 |
Строим планы механизма (рис.3.2).
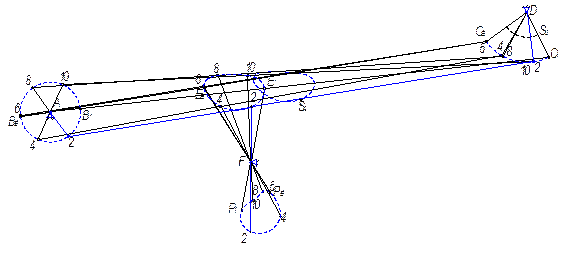
Рис. 3.2. Планы механизма.
3.3 Кинематическое исследование машин и механизмов
аналитическим методом.
3.2.2. Кинематическое исследование механизма аналитическим методом.
Для определения кинематических характеристик механизма применим метод замкнутых векторных контуров.
1. Рисуем во втором промежуточном положении структурную схему исследуемого механизма.
2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.
3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.
4. Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры: ABD, BCD, ABEF (рис.3.3)

Рис. 3.3. Построение векторных контуров
5. Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора AB. Все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие - со знаком «–»:
![]() (3.1)
(3.1)
Уравнению (3.1) соответствуют два уравнения проекций на оси координат:
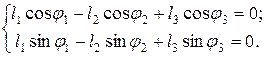 (3.2)
(3.2)
Среди величин, входящих в уравнение (3.2) переменными
являются углы ![]() ,
, ![]() и длина l3. Угол
и длина l3. Угол ![]() является
обобщенной координатой механизма. Решив уравнения (3.2) получим:
является
обобщенной координатой механизма. Решив уравнения (3.2) получим:
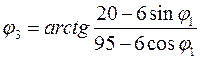 ;
(3.3)
;
(3.3)
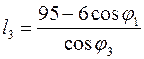 (3.4)
(3.4)
Рассмотрим контур BCD, уравнение замкнутости которого имеет вид:
![]() (3.5)
(3.5)
Спроецировав это векторное уравнение на оси координат получим:
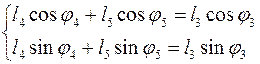 (3.5)
(3.5)
Решив эту систему
найдем углы ![]() и
и ![]() :
:
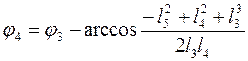 (3.6)
(3.6)
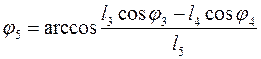 (3.7)
(3.7)
Уравнение замкнутости третьего контура ABEF имеет вид:
![]() (3.8)
(3.8)
или в проекциях на оси координат:
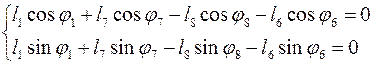 (3.9)
(3.9)
Решив систему
(3.9) найдем угол ![]() и модуль
и модуль
![]() .
.
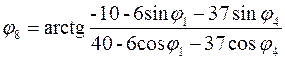 (3.10)
(3.10)
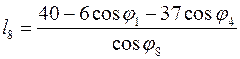 (3.11)
(3.11)
Для нахождения
положений точек ![]() и
и ![]() записываем
уравнения замкнутости контуров ABS2A и ABCS3A (рис. 3.3):
записываем
уравнения замкнутости контуров ABS2A и ABCS3A (рис. 3.3):
![]() (3.12)
(3.12)
![]() (3.13)
(3.13)
Из уравнений (3.12) и (3.13) находим координаты центров масс звеньев 2 и 3:
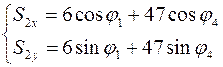 (3.14)
(3.14)
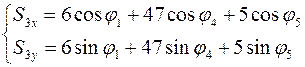 (3.15)
(3.15)
Рассчет положений звеньев
Т а б л и ц а (3.1)
|
Величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
Начало |
6,324 |
0,110 |
0,214 |
0,911 |
0,110 |
2,025 |
1,387 |
0,150 |
0,527 |
0,058 |
0,972 |
0,155 |
|
Рабочий ход |
0,000 |
0,000 |
0,221 |
0,912 |
0,117 |
2,021 |
1,381 |
0,146 |
0,527 |
0,055 |
0,972 |
0,155 |
|
350,000 |
6,109 |
0,232 |
0,915 |
0,127 |
1,998 |
1,382 |
0,139 |
0,525 |
0,049 |
0,971 |
0,155 |
|
|
340,000 |
5,934 |
0,242 |
0,920 |
0,136 |
1,957 |
1,396 |
0,132 |
0,522 |
0,043 |
0,969 |
0,154 |
|
|
330,000 |
5,760 |
0,251 |
0,927 |
0,144 |
1,898 |
1,425 |
0,125 |
0,517 |
0,038 |
0,966 |
0,153 |
|
|
320,000 |
5,585 |
0,258 |
0,935 |
0,151 |
1,826 |
1,471 |
0,118 |
0,511 |
0,032 |
0,963 |
0,152 |
|
|
310,000 |
5,411 |
0,264 |
0,944 |
0,157 |
1,741 |
1,535 |
0,112 |
0,503 |
0,028 |
0,958 |
0,151 |
|
|
300,000 |
5,236 |
0,267 |
0,954 |
0,163 |
1,647 |
1,616 |
0,108 |
0,494 |
0,024 |
0,954 |
0,150 |
|
|
290,000 |
5,061 |
0,269 |
0,964 |
0,167 |
1,545 |
1,709 |
0,106 |
0,484 |
0,022 |
0,949 |
0,150 |
|
|
280,000 |
4,887 |
0,269 |
0,975 |
0,171 |
1,437 |
1,807 |
0,107 |
0,474 |
0,021 |
0,943 |
0,150 |
|
|
270,000 |
4,712 |
0,267 |
0,985 |
0,174 |
1,326 |
1,900 |
0,110 |
0,463 |
0,021 |
0,938 |
0,151 |
|
|
260,000 |
4,538 |
0,263 |
0,995 |
0,177 |
1,212 |
1,982 |
0,116 |
0,452 |
0,024 |
0,932 |
0,153 |
|
|
250,000 |
4,363 |
0,258 |
1,004 |
0,179 |
1,098 |
2,047 |
0,123 |
0,442 |
0,027 |
0,927 |
0,155 |
|
|
240,000 |
4,189 |
0,252 |
1,012 |
0,180 |
0,985 |
2,094 |
0,132 |
0,432 |
0,032 |
0,922 |
0,158 |
|
|
230,000 |
4,014 |
0,244 |
1,019 |
0,181 |
0,878 |
2,125 |
0,142 |
0,424 |
0,039 |
0,918 |
0,162 |
|
|
220,000 |
3,840 |
0,235 |
1,024 |
0,180 |
0,779 |
2,141 |
0,152 |
0,416 |
0,046 |
0,914 |
0,165 |
|
|
210,000 |
3,665 |
0,226 |
1,028 |
0,177 |
0,697 |
2,146 |
0,161 |
0,411 |
0,053 |
0,912 |
0,168 |
|
|
200,000 |
3,491 |
0,216 |
1,030 |
0,172 |
0,639 |
2,142 |
0,170 |
0,407 |
0,060 |
0,910 |
0,170 |
|
|
Конец |
189,295 |
3,304 |
0,205 |
1,031 |
0,162 |
0,617 |
2,131 |
0,177 |
0,405 |
0,066 |
0,909 |
0,171 |
|
Холостой ход |
180,000 |
3,142 |
0,195 |
1,030 |
0,150 |
0,633 |
2,116 |
0,182 |
0,405 |
0,070 |
0,910 |
0,170 |
|
170,000 |
2,967 |
0,186 |
1,027 |
0,135 |
0,682 |
2,094 |
0,185 |
0,407 |
0,074 |
0,911 |
0,168 |
|
|
160,000 |
2,793 |
0,176 |
1,022 |
0,118 |
0,753 |
2,067 |
0,187 |
0,410 |
0,076 |
0,914 |
0,166 |
|
|
150,000 |
2,618 |
0,168 |
1,016 |
0,102 |
0,839 |
2,035 |
0,187 |
0,416 |
0,078 |
0,917 |
0,163 |
|
|
140,000 |
2,443 |
0,161 |
1,009 |
0,086 |
0,934 |
1,997 |
0,187 |
0,422 |
0,079 |
0,920 |
0,160 |
|
|
130,000 |
2,269 |
0,155 |
1,000 |
0,072 |
1,035 |
1,953 |
0,186 |
0,430 |
0,080 |
0,924 |
0,157 |
|
|
120,000 |
2,094 |
0,150 |
0,991 |
0,061 |
1,140 |
1,906 |
0,185 |
0,439 |
0,081 |
0,929 |
0,155 |
|
|
110,000 |
1,920 |
0,147 |
0,981 |
0,052 |
1,247 |
1,854 |
0,183 |
0,449 |
0,081 |
0,934 |
0,153 |
|
|
100,000 |
1,745 |
0,146 |
0,971 |
0,046 |
1,355 |
1,799 |
0,181 |
0,459 |
0,081 |
0,939 |
0,151 |
|
|
90,000 |
1,571 |
0,146 |
0,960 |
0,043 |
1,462 |
1,742 |
0,179 |
0,470 |
0,080 |
0,945 |
0,150 |
|
|
80,000 |
1,396 |
0,149 |
0,950 |
0,044 |
1,566 |
1,684 |
0,176 |
0,480 |
0,080 |
0,950 |
0,150 |
|
|
70,000 |
1,222 |
0,153 |
0,941 |
0,047 |
1,666 |
1,628 |
0,174 |
0,490 |
0,078 |
0,955 |
0,150 |
|
|
60,000 |
1,047 |
0,160 |
0,932 |
0,053 |
1,759 |
1,574 |
0,172 |
0,499 |
0,077 |
0,959 |
0,151 |
|
|
50,000 |
0,873 |
0,167 |
0,924 |
0,061 |
1,842 |
1,524 |
0,169 |
0,508 |
0,075 |
0,963 |
0,152 |
|
|
40,000 |
0,698 |
0,177 |
0,918 |
0,072 |
1,913 |
1,480 |
0,166 |
0,515 |
0,072 |
0,967 |
0,153 |
|
|
30,000 |
0,524 |
0,187 |
0,914 |
0,083 |
1,969 |
1,443 |
0,162 |
0,520 |
0,069 |
0,969 |
0,154 |
|
|
20,000 |
0,349 |
0,198 |
0,911 |
0,095 |
2,006 |
1,413 |
0,157 |
0,524 |
0,065 |
0,971 |
0,155 |
|
|
10,000 |
0,175 |
0,210 |
0,911 |
0,106 |
2,024 |
1,392 |
0,152 |
0,526 |
0,060 |
0,972 |
0,155 |
|
|
Начало |
6,324 |
0,110 |
0,214 |
0,911 |
0,110 |
2,025 |
1,387 |
0,150 |
0,527 |
0,058 |
0,972 |
0,155 |
Результаты расчета положений звеньев
Т а б л и ц а (3.2)
|
Величина |
|
|
|
|
|
|
|
|
Графически |
300 |
15,31611 |
95,387872 |
9,32114 |
94,35194 |
92,59086 |
0,10807708 |
|
Аналитич. |
300 |
15,31611 |
95,387872 |
9,32114 |
94,35194 |
92,59086 |
0,10807708 |
|
Откл, % |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Найдем аналоги
скоростей и ускорений. Так как они не зависят от закона изменения обобщенной
координаты, принимаем ![]() .
.
Аналитическое
определение аналогов скоростей основано на дифференцировании по обобщенной
координате уравнений (3.2), (3.5) и (3.9). После дифференцирования (3.2),
учитывая, что вектор ![]() не зависит от обобщенной координаты, получим:
не зависит от обобщенной координаты, получим:
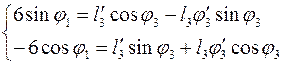 (3.16)
(3.16)
где ![]() ,
, ![]() - аналоги угловых скоростей звеньев 1 и 3,
- аналоги угловых скоростей звеньев 1 и 3, ![]() - аналог поступательной скорости звена 3.
- аналог поступательной скорости звена 3.
Решая
(3.16) находим соответственно ![]() и
и ![]() :
:
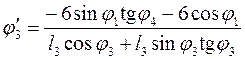 (3.17)
(3.17)
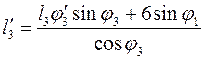 (3.18)
(3.18)
Дифференцируя (3.5) получаем:
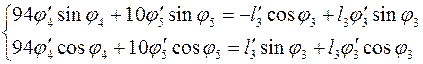 (3.19)
(3.19)
Решив (3.19)
найдем ![]() и
и ![]() соответственно:
соответственно:
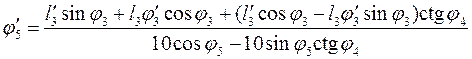 (3.20)
(3.20)
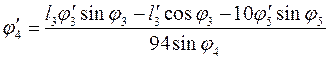 (3.21)
(3.21)
Дифференцируя (3.9) получим:
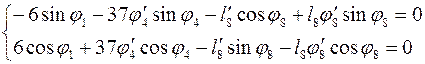 (3.22)
(3.22)
Решив (3.22) найдем ![]() и
и ![]() соответственно:
соответственно:
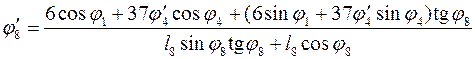 (3.23)
(3.23)
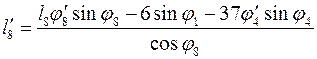 (3.24)
(3.24)
Аналоги скоростей центров масс звеньев 2 и 3 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (3.14) и (3.15):
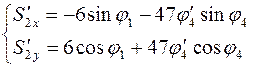 (3.25)
(3.25)
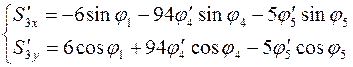 (3.26)
(3.26)
Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (3.16), (3.19) и (3.22)
Для первого контура:
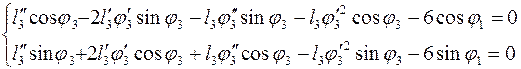 (3.27)
(3.27)
Вычтя из всех тригонометрических функций угол ![]() , получим:
, получим:
![]() (3.28)
(3.28)
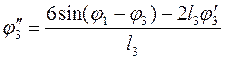 (3.29)
(3.29)
Для второго контура:
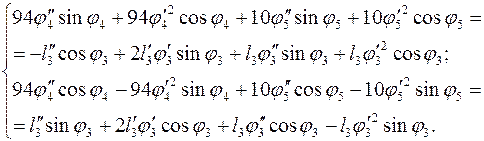 (3.30)
(3.30)
Вычтя из всех тригонометрических функций первого уравнения
угол ![]() , а затем
, а затем ![]() , получим:
, получим:
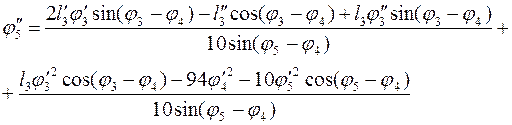 (3.31)
(3.31)
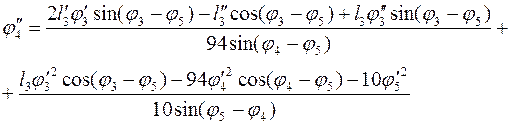 (3.32)
(3.32)
Для третьего контура запишем только одну производную системы (3.22):
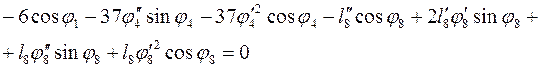 (3.33)
(3.33)
Вычтя угол ![]() получим:
получим:
![]() (3.34)
(3.34)
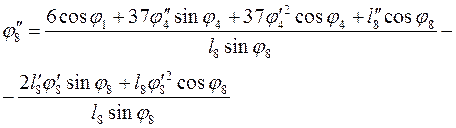 (3.35)
(3.35)
Дифференцируя по обобщенной координате уравнения (3.25) и (3.26), устанавливаем аналоги ускорений центров масс звеньев 2 и 3 в проекциях на оси координат:
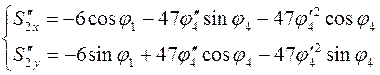 (3.36)
(3.36)
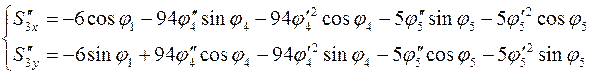
(3.37)
3.4 Построение планов скоростей и ускорений.
3.4.1. Определение аналогов скоростей исследуемого станка графическим методом.
Построим план скоростей
для положения ![]() . Так как
аналоги скоростей не зависят от закона изменения обобщенной координаты,
принимаем
. Так как
аналоги скоростей не зависят от закона изменения обобщенной координаты,
принимаем ![]() .
.
План скоростей механизма строим в следующем порядке:
1) находим скорость тачки B:
![]() ;
;
2) из полюса плана скоростей p откладываем отрезок pb=60см, изображающий вектор скорости точки B (рис. 3.4);
3) подсчитываем масштабный коэффициент скоростей:
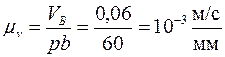 ;
;
4) Для определения скорости точки C раскладываем плоскопараллельное движение звена 2 на переносное (поступательное) вместе с точкой B и относительное (вращательное) вокруг точки B. С другой стороны, точка C находится в относительном движении вокруг неподвижной точки D. Поэтому
![]() (3.38)
(3.38)
Уравнение (3.38) решаем графически. Через точку B проводим линию, перпендикулярную CB,
а через полюс P – линию, перпендикулярную CD, до их пересечения в точке c.
Векторы ![]() и
и ![]() изображают искомые векторы
изображают искомые векторы ![]() и
и
![]() ;
;

Рис. 3.4. План скоростей исследуемого механизма
5) Скорость точки E определяем, используя теорему подобия
6)
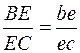 ,
,
вектор ![]() изображает искомый вектор
изображает искомый вектор ![]() ;
;
7) Скорость точки P находим как сумму поступательной скорости звена
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.