Необходимый момент инерции маховика подсчитываем по формуле
![]() (4.12)
(4.12)
Так как касательные не пересекают ось ![]() в
пределах чертжа, то отрезок ab
находим из соотношения
в
пределах чертжа, то отрезок ab
находим из соотношения
4.5 Определение угловой скорости и углового ускоения начального звена механизма.
Угловую скорость звена приведения механзма находим по формуле:
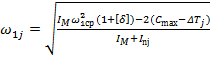 (4.13)
(4.13)
Результаты расчетов заносим в таблицу 4.1
Угловоеускорение звена приведения механизма находим по формуле:
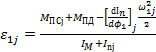 (4.14)
(4.14)
Результаты расчета ![]() заносим
в таблицу 4.1.
заносим
в таблицу 4.1.
5. Силовой анализ мханизма качающегося конвейера
При силовом анализе механизма действующие силы должны быть известны, а подлежат определению уравновешивающий момент и реакции во всех кинематических парах. Решение этх задач основано на применении принципа Даламбера, согласно которомузвено механизма можно рассматривать как находящееся вравновесии, если ко вем внешним силам, действующим на него, добавить силы инерции.
Силовой анализмеханизма проводится для того, чтобы впоследствии по найденным силам (моментам) произвести расчет на прочность элементов кинематических пар и звеньев механизма, а также правильно подобрать привод.
5.1 Определение сил, действующих на механизм
5.1.1 Определение сил инерции.
Определим проекции ускорений центров тяжести звеньев на оси координат по формулам:
![]() (5.1)
(5.1)
![]() (5.2)
(5.2)
![]() (5.3)
(5.3)
Расчет производим для положения 3 механизма
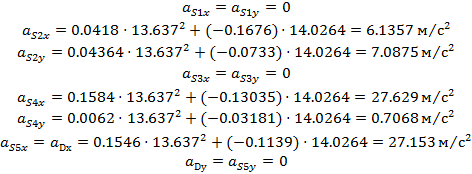
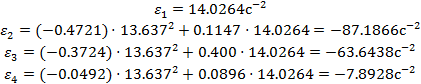
Определив ускорения определяем главые векторы сил инерции и главный инерционный момент звеньв механизма по формулам
![]() (5.4)
(5.4)
![]() (5.5)
(5.5)
![]() (5.6)
(5.6)
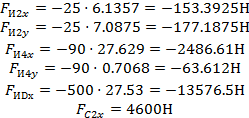
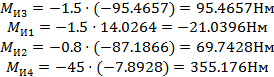
Так как направления сил и моентов учтены их знаками, то а расчетных схемахвсе силы изображаем в направлени координатных осей, а моменты – противхода селки часов.
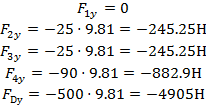
5.2 Определение уравнвешивающего момента и реакций в кинематических парах аналитическимметодом.
Силовой анализ механзма аналитичесим методом проводтся поледовательно и отделно для каждой структурной групы, начиная сой, в коорую входит выходное звено. Началное звено анализруется последним.
Для определения реакций в кинематических парах струкурных групп и началного звена составляются и решаются уравнения статики. Причем на первом этапенаходятся реакци во внешних кинематических парах, а затем во внутренних.
5.2.1 Силовой анализ структурной группы 4–5.
Прикладываем к структурной группе 4-5 с цлью упрощения вычислений в проекцях на оси действующие на не силы (рис. 5.1)
![]()
![]() (5.7)
(5.7)
![]() ,
,
![]() (5.8)
(5.8)
![]() ,
,
![]() (5.9)
(5.9)
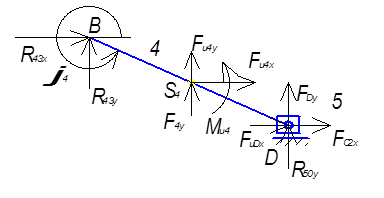
Рис. 5.1
Из уравнения (5.7) находим реакции ![]()
Из уравнения (5.8) находим реакции ![]()
Из уравнения (5.9) находим реакции ![]()
![]()
Для оределения оответствующих ракций внутренней в суктурной группе 4-5 рассмотрим в равновеси звено 5 (рис. 5.2)
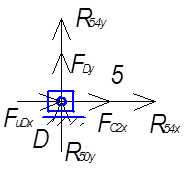 Рис.
5.2
Рис.
5.2
![]() ,
,
![]() (5.10)
(5.10)
![]() ,
,
![]() (5.11)
(5.11)
Из уравнения (5.10) находим реакции ![]()
Из уравнения (5.11) находим реакции ![]()
![]()
5.2.2 Силовой аналз структурной группы 2–3.
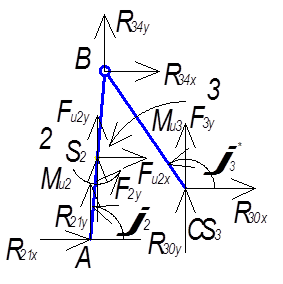 Аналогично
предыдущему прикладываем к структурной группе 2-3 действующие на не силы.
Очевидно, что
Аналогично
предыдущему прикладываем к структурной группе 2-3 действующие на не силы.
Очевидно, что ![]() и
и
![]() (рис.
5.3)
(рис.
5.3)
Рис. 5.3
![]() ,
,
![]() (5.12)
(5.12)
![]() ,
,
![]() (5.13)
(5.13)
![]() ,
,
![]() (5.14)
(5.14)
![]() ,
,
![]() (5.15)
(5.15)
Из уравнений (5.12) и (5.13) находим
проекции реакции ![]() и
и
![]()
![]()
![]()
![]()
Из уравнений (5.14) находим проекции
реакции ![]()
Из уравнений (5.15) находим проекции
реакции ![]()
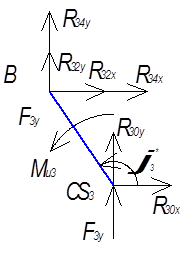 Для
оределения прокций ракции
Для
оределения прокций ракции ![]() внутренней
в суктурной группе 2-3 рассмотрим в равновеси звено BC
(рис. 5.4)
внутренней
в суктурной группе 2-3 рассмотрим в равновеси звено BC
(рис. 5.4)
Рис. 5.4
![]() ,
,
![]() (5.16)
(5.16)
![]() ,
,
![]() (5.17)
(5.17)
Из уравнения (5.16) определем проекцию ![]()
Из уравнений (5.17) опредляем проекцию ![]()
![]()
5.2.3 Определение уавновешвающего момента ![]() и
реакции
и
реакции ![]() в
кинемтичской паре O.
в
кинемтичской паре O.
Прикладываем к звену ОА дейтвующие силы,
реакции и моменты. Очвидно, что ![]() и
и
![]() (рис.
5.5).
(рис.
5.5).
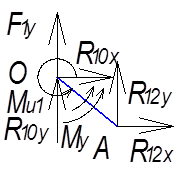 Рис.
5.5
Рис.
5.5
Рассматриваем звено ОА в равновеии.
![]() ,
,
![]() (5.18)
(5.18)
![]() ,
,
![]() (5.19)
(5.19)
![]() ,
,
![]() (5.20)
(5.20)
Из уравнения (5.18) определем проекцию ![]()
Из уравнений (5.19) опредляем проекцию ![]()
![]()
Из уравнения (5.20) определем проекцию ![]()
5.3 Определние уравновешивабщегомомента методом ычага Жуковского.
Теорема Н. Е. Жуковскоо применяется при решении многих задач динамики машин. В частности, она используется для определния уравновешивающего момента, если нет необходимости в последовательном определении реакцийв кинематическихпарах механизма.
Теорема Жуковского гласит: «Если силу, приложенную к какой-либо точке звена механизма, перенести параллельно самой себе в одноименную точку перевернутогопланаскоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности, т. е.
![]() (5.21)
(5.21)
где
![]() –
момент силы
–
момент силы ![]() относительно
полюса скоростей,
относительно
полюса скоростей,
![]() -
мощность силы
-
мощность силы ![]() .
.
Из законов динамики следует, что сумма мощностей всех внешних сил и сил инерции звеньев, приложенных и механизму, рвна нулю, или
![]() (5.22)
(5.22)
В соответствии с теоремой Жуковского последнее уравнение равносильно уравнению моментов относительно полюса повернутого плана скоростей, т. е.
![]() (5.23)
(5.23)
Из уравнения (5.23) находится уравновешивающий момент (уравновешивающая сила).
Сосавим и решим (5.23) для качающегося ковейера в 3-ем положении механизма. Строим поернутый на 90° план скоростей механизма, к которому в соответствующих точках прикладываем заданные силы и силы инерции, сохраня их истиные направления.
Моменты инции ![]() ,
,
![]() ,
,
![]() ,
,
![]() замняем
парами сил
замняем
парами сил ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() соответственоо,
которые прикладываем перпендкулярно орезкам OA,
AB,
BC,
BD.
Модули этих сил определяется:
соответственоо,
которые прикладываем перпендкулярно орезкам OA,
AB,
BC,
BD.
Модули этих сил определяется:
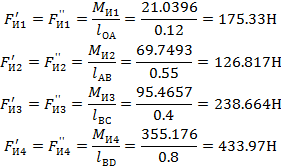
Записываем уравнение (5.23) моментов сил относительно полюса плана скоростей:
![]() (5.24)
(5.24)
![]()
Зная величину ![]() ,
найдем уравновешивающий момент
,
найдем уравновешивающий момент ![]()
Отклонение найденного с помощью рычага Жуковсккого значения момента
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.