|
|
|
|
|
 |
КАФЕДРА ПРИКЛАДНОЙ МЕХАНИКИ
к курсовому проекту по теории машин и механизмов
на тему: Анализ и синтез механизмов формовочной машины
Автор проекта Ф.И.О.
Специальность 1705
Обозначение проекта КП--40-14-01
Группа МХ –91
Руководитель проекта
Проект защищен Оценка
1. Задание на проект
Выполнить структурный, кинематический и динамический анализ механизма формовочной машины.
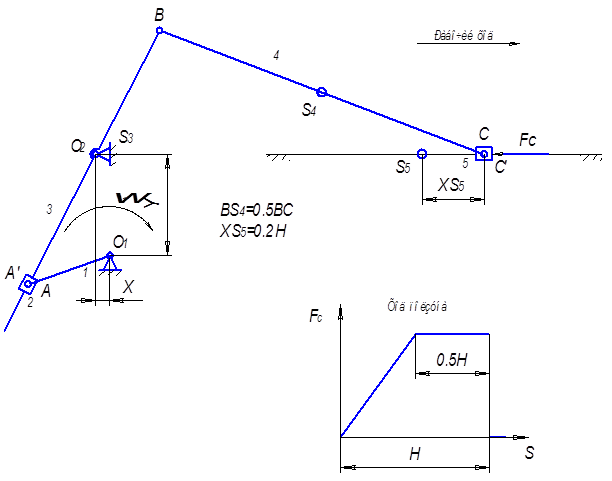
Рис. 1.1. Задание на анализ и синтез строгального станка.
Таблица 1.1
|
lOA, м |
LBC, м |
lCD, м |
wd, рад/с |
X,м |
|
0,35 |
0,28 |
1,25 |
150 |
0,11 |
Продолжение таблицы 1.1
|
m3, кг |
m4, кг |
m5, кг |
JO1, кг×м2 |
JS3, кг×м2 |
JS4, кг×м2 |
Jd, кг×м2 |
FC, H |
d |
|
10 |
18 |
300 |
0,55 |
1,80 |
4,00 |
0,15 |
600 |
0,40 |
2. Структурный анализ механизма формовочной машины
2.1. Структурная схема машины
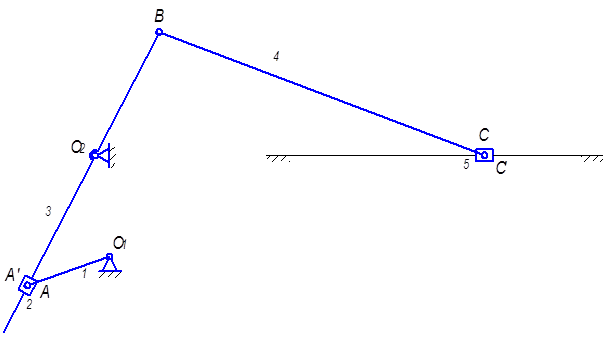
2.2. Выявление сложных и разнесенных кинематических пар
В механизме формовочной машины сложных и кинематических пар нет.
2.3. Классификация кинематических пар механизма
Таблица 2.1
|
№ п/п |
Номера звеньев, образую-щих пару |
Условное обозначение |
Название |
Подвиж- ность |
Высшая/ Низшая |
Замыкание (Геометри-ческое/ Силовое) |
Открытая/ Закрытая |
|
1 |
0 – 1 |
|
Вращатель-ная |
1 |
Н |
Г |
З |
|
2 |
1 – 2 |
|
Вращатель-ная |
1 |
Н |
Г |
З |
|
3 |
2 – 3 |
|
Поступа- тельная |
1 |
Н |
Г |
З |
|
4 |
3 – 0 |
|
Вращатель-ная |
1 |
Н |
Г |
З |
|
5 |
3 – 4 |
|
Вращатель-ная |
1 |
Н |
Г |
З |
|
6 |
4 – 5 |
|
Вращатель-ная |
1 |
Н |
Г |
З |
|
7 |
5 – 0 |
|
Поступа- тельная |
1 |
Н |
Г |
З |
Исследуемый механизм состоит только из одноподвижных кинематических пар (р1 = 7, р = 7), где р1 – число одноподвижных кинематических пар в механизме, р - общее число кинематических пар в механизме.
2.4. Классификация звеньев механизма
Звеном называется деталь или несколько неподвижно соединенных между собой деталей, движущихся как единое целое.
Механизм имеет: четыре (n2 = 4) двухвершинных (t = 2) линейных звена 1, 2, 4, 5; одно (n3 = 1) трехвершинное (t= 3) звено 3, которое является базовым (T = 3); пять (n = 5) подвижных звеньев.
Таблица 2.2
|
№ п/п |
Номер звена |
Условное обозначение |
Название |
Движение |
Число вершин (t) |
|
1 |
0 |
|
Стойка |
- |
- |
|
2 |
1 |
|
Кривошип |
Враща-тельное |
2 |
|
3 |
2 |
|
Камень (2) |
Сложное |
2 |
|
4 |
3 |
|
Кулиса (3) (коромыс-ло) |
Враща-тельное |
3 |
|
5 |
4 |
|
Шатун (4) |
Сложное |
2 |
|
6 |
5 |
|
Ползун |
Поступа-тельное |
2 |
2.5. Нахождение числа присоединений к стойке
Механизм формовочной машины имеет три (S = 3) присоединения к стойке.
2.6. Выделение в машине простых, элементарных и с разомкнутыми цепями механизмов
В исследуемом сложном механизме можно выделить один элементарный механизм
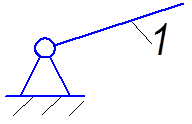
и два простых, один из которых является кулисным,
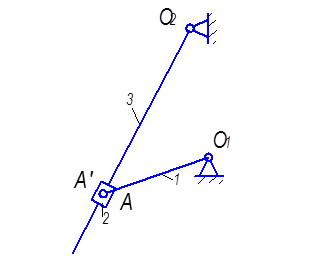
а второй кривошипно – ползунным
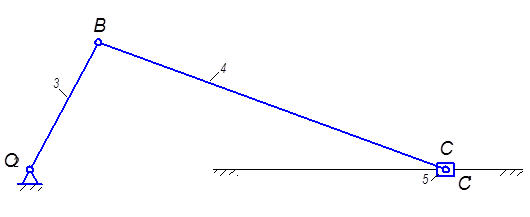
Механизмов с разомкнутыми кинематическими цепями в исследуемой формовочной машине нет.
2.7. Выявление простых стационарных и подвижных механизмов
Машина имеет в своем составе только простые стационарные механизмы.
2.8. Выявление звеньев закрепления и присоединения
В исследуемом сложном механизме формовочной машины звеньев закрепления нет. У него есть только одно звено присоединения – звено 3 (кулиса). Звено 3 одновременно входит в два простых механизма – кулисный и кривошипно-ползунный. Значит, для этого звена К3 = 2.
2.9. Классификация механизма машины
Исследуемый механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеют в своем составе только замкнутые кинематические цепи.
2.10. Определение подвижности простых механизмов машины
Анализ движений звеньев механизма и элементов кинематических пар показывает, что исследуемые простые механизмы, да и сам сложный механизм существуют в трехподвижном (П = 3) пространстве, в котором разрешены следующие простейшие независимые движения: два поступательных xи y вдоль соответствующих осей; одно вращательное jz вокруг оси Z.
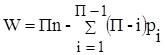 ;
; 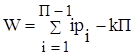 ,
(2.1)
,
(2.1)
где W – подвижность механизма; П – подвижность пространства, в
котором существует исследуемый механизм; n – число подвижных звеньев механизма; i – целочисленный индекс; pi – число кинематических пар i-й подвижности; k = p – n – число независимых контуров; 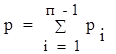 - общее число кинематических
пар в механизме.
- общее число кинематических
пар в механизме.
Формулы для определения подвижности этих механизмов примут вид соответственно:
W = 3n – 2p1 – p2;
W = p1 – 2p2 – 3k;
k = p – n.
Определим подвижность кулисного механизма. Этот механизм имеет: три (n = 3) подвижных звена 1, 2, 3 и четыре (p = p1 = 4) кинематические пары O1, A, A’, O2. Тогда его подвижность определится:
Wк = 3×3 – 2×4 = 1;
k = 4 – 3 = 1;
Wк = 4 – 3×1 = 1.
Найдем подвижность кривошипно-ползунного механизма. Кривошипно – ползунный механизм имеет: три (n = 3) подвижных звена 3, 4, 5 и четыре (p = p1 = 4) кинематические пары O2, B, C, C’. Так как кривошипно – ползунный механизм по количественному и качественному составу кинематических пар и звеньев ничем не отличается от кулисного механизма, то его подвижность определится по тем же формулам и также равна единице (Wкп = 1).
2.11. Подвижность механизмов с незамкнутыми кинематическими цепями
Так как в станке нет механизмов с незамкнутыми кинематическими цепями, то нет и необходимости определять их подвижность.
2.12. Определение подвижности сложного механизма
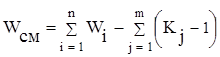 , (2.2)
, (2.2)
где Wсм – подвижность сложного механизма; i – индекс, порядковый номер простого механизма; Wi – подвижность i-го простого механизма; n – общее число простых механизмов, входящих в состав сложного; j – индекс общего звена; m – суммарное число общих звеньев; K – число присоединений к j-му общему звену простых механизмов.
Подвижность сложного механизма долбежного станка определится
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.