Анализ и синтез механизмов комбайна (Силовой анализ)

4. Силовой анализ механизма.

4.1 Силовой анализ механизма аналитическим методом

4.1.1 Силовой анализ структурной группы 4-5.

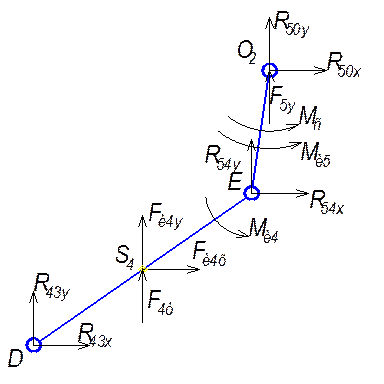
F_kx=R_43x +F_И4x+R_50x=0, откуда R_43x -2,725+R_50x=0

F_ky=R_43y +F_И4y+F_4y+F_5y + R_50y =0, откуда R_43y -577,185 + R_50y =0

(F _к) = -R_43y l_DЕ cos(φ₅)+R_43хl_DЕ sin(φ₅)-F_4yl_ЕS4cos(φ₅)-F_И4y l_ЕS4cos(φ₅)-F_И4x l_ЕS4sin(φ₅ )+M_И4=0, откуда -1,2247R_43y +0,2504R_43х+300,0331+5,3793+0,3412+0,7305=0,

-1,2247R_43y +0,2504R_43х+306,484=0

(F_к)= (R_50y +F_5y )l_О2Е cos(φ₆)-R_50xl_O2E sin(φ₆)+M_c +M_И5=0 откуда     0,05664R_50y -0,8581R_50x- 4,4403-50 -0,08254=0

0,05664R_50y -0,8581R_50x- 54,5228=0

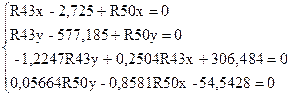
R_43х  =45,296

R_43y  =259,513

R_50x  = - 42,571

R_{50y   = 317,672}             

Реакции во внутренней кинематической паре Е определяем из условия равновесия звена 5:

 =R_50x  +R_54x=0              (3.10)

  = F_5y + R_50y+ R_54y =0             (3.11)

откуда R_54x= -R_50x= 42,571

R_54y= - F_5y -R_50y=78,4- 317,672= -239,272

Таким образом, реакции в кинематических парах группы 4-5

пара D :   R₄₃==263,436H

пара Е R₄₅=  Н

пара О₂         R₅₀=  Н

4.1.2 Силовой анализ структурной группы 2-3

R_34X= -R_43X= -45,296

R_34Y= -R_43Y= -259,513        

Условия равновесия группы 2-3

F_kx=R_21x +F_И2x+R_30x+ R_34x =0, откуда   R_21x +R_30x +0,5336-45,296 = 0,

R_21x +R_30x -44,762 = 0

F_ky=R_21y +F_2y+ F_И2y+R_30y + R_34y =0, откуда   R_21y -78,4-0,1208+R_30y -259,513= =0,  R_21y +R_30y – 338,034= 0,

(F_к)= -R_21y l_AВ cosφ₂+R_21xl_АВ sinφ₂–(F_2y+F_И2y)l_BS2cosφ₂+F_И2хl_BS2sinφ₂+M_И2 =0, откуда  -0,9425R_21y +0,3342R_21x–(-78,4-0,1208)0,4713+0,0892+0,5738 =0

-0,9425R_21y +0,3342R_21x+37,67 =0

 (F_к)=-R_30yl_OBcos(φ₃-180)+R_30хl_0Bsin(φ₃-180)-R_34yl_BDcos(φ₃-180)+R_34хl_BDsin(φ₃-180)=0 откуда                

-0,07688R_30y +0,4434R_30х+51,4288 -51,771=0

-0,07688R_30y +0,4434R_30х-0,3422=0

R_{21x =-8,194 H}

R_{21y =37,063 H}

R_{30х =52,956 H}

R_{30y =300,971 Н}

    Реакция во внутренней кинематической паре определяется из условия равновесия звена 3

=R_32x +R_30х+R_34x =0, откуда

R_32x +52,956-45,296 =0,   R_32x = -7,66 H

 =R_32y + R_30y + R_34y =0, откуда

R_32y + 300,971 -259,513 =0,   R_32y =-41,458 H

Таким образом, реакции в кинематических парах группы 2 - 3:

пара А: R₂₁= Н

параВ: R₂₃= Н

параО: R₃₀= Н

 

  4.1.3 Силовое исследование начального звена

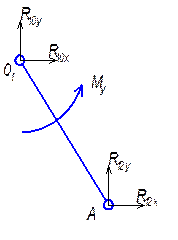
R_12x= -R_21x = 8,194  H;               R_12y= - R_21y=-37,063  H

Условия равновесия начального звена

M₀₁ (F _к) =R_12х× l_01А ×sin(360-φ₁) + R_12y ×l_01А×cos(360-φ₁) + M_y=0   

F_кх = R_10х + R_12х=0

F_ку = R_10y+ R_12y=0

R_10х=-R_12х= -8,194  Н

R_10у= - R_12у = 37,063  Н

Нм-уравновешивающий момент .

Реакция в кинематической паре О₁ :

R₁₀ =Н

4.2.Силовой анализ механизма графическим методом

4.2.1 Силовой анализ структурной группы  4-5.

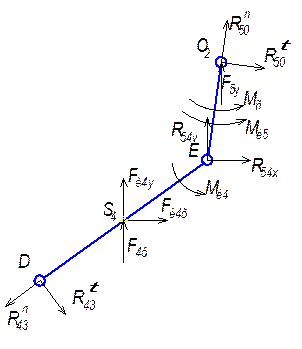
Реакцию  определим из условия равновесия звена 4:

(F _к) = 

Н

Реакцию  определим из условия равновесия звена 5:

Н

Реакции иопределим из условия равновесия группы :

Принимаем масштабный коэффициент μ=5 Н/мм. Тогда:

(аb)=

(bc)=

(сd)=

(de)=

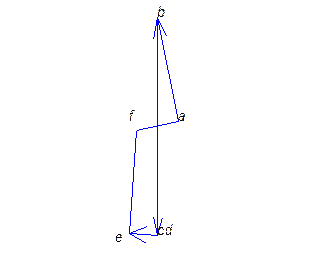
(af)=19,746мм

(ef)=62,73мм

Н

=263,22 Н

Н

Н

Реакцию во внутренней кинематической паре Е определяем графически, в соответствии с условием равновесия звена 5:

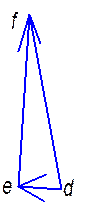
(df)=48,92мм

F54 =244,6 H

Данные полученные в результате расчетов графическим и аналитическим методом, сводим в табл. 4.2

Таблица 4.2

Сравнительный анализ графического и аналитического расчетов

Величина	R43	R45	R50
Аналитический	263,44	243,03	320,51
Графический	262,22	244,60	320,12
Отклонение %	0,46	0,64	0,12

4.2.2 Силовой анализ структурной группы  2-3.

Реакцию   определим из условия равновесия звена 2:

  

Н

Реакцию  определим из условия равновесия звена 3:

Н

Реакции иопределим из условия равновесия группы :

Принимаем масштабный коэффициент μ=3 Н/мм. Тогда:

(аb)=

(bc)=

(сd)=

(de)=

                                   

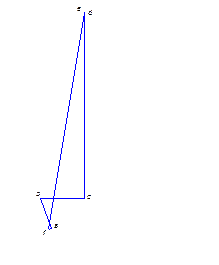
(af)=1,126мм

(ef)=87,627мм

Н          Н       

Н            Н

Реакцию во внутренней кинематической паре B определяем графически, в соответствии с условием равновесия звена 3:

(ab)=

(bc)=

(cd)=

(de)=

(ea)=14,24мм                   R23=42,72 H

Величина	R21	R23
Аналитический	37,958	42,16
Графический	37,906	42,72
Отклонение %	0,14	1,31

          4.2.3.Силовой анализ начального звена

Изображаем в масштабе μ_l= 5×10^-3 м/мм начальное звено, прикладывая к нему реакцию R ₁₂, найденную при анализе группы 2-3 , реакцию R₁₀ и уравновешивающий момент М_у

М_уопределяем из условия равновесия начального звена:

(F_k) = М_у-R₁₂ h μ_l=0, где h=17,145 мм

М_у= R₁₂ h μ_l=37,953×17,145×5×10^-3=3,2535 Н×м – по часовой стрелке

Реакцию R₁₀  определим из уравнения :

R₁₂+R₁₀=0, откуда R₁₀ =-R₁₂, R₁₀= R₁₂=37,953 Н

Находим погрешность определения уравновешивающего момента М_у :

4.3. Определение уравновешивающего момента методом рычага

Жуковского

Теорема Жуковского используется для определения уравновешивающего момента, когда не требуется последовательного определения реакций в кинематических парах механизма.

Теорема Жуковского: Если силу, приложенную к какой- либо точке звена механизма, перенести параллельно самой себе в одноименную точку повернутого плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности, т. е.

М_Р(F_i)=P_i , где М_Р- момент силы F_i относительно полюса плана скоростей, P_i- мощность силы F_i.

Так как сумма мощностей всех внешних сил и сил инерции звеньев, приложенных к механизму равна нулю, то уравнение равносильно:

åМ_Р(F_i)+åМ_Р(F_и)=0

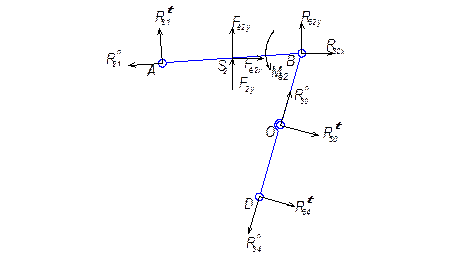
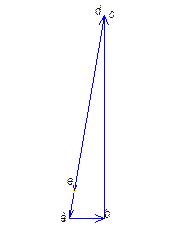
Составим и решим уравнение. Строим повернутый на 90° план скоростей механизма, к которому в соответствующих точках прикладываем заданные силы и силы инерции.

Моменты инерции Ми₂ Ми₄ Ми₅ заменяем парами сил

 Fи₂ Fи₂', Fи₄ Fи₄', Fи₅ Fи₅' соответственно, которые прикладываем перпендикулярно отрезкам АВ, DE, EO₂ в кинематических парах А,В,D, Е, О₂. Модули этих сил определятся:

F^/_с=М_с/l_О2Е=50/0,86=58,1395 H

 

F^/_и2=М_и2/l_АВ=0,5738/1=0,5738 H

      F^/_и4=М_и4/l_DE=0,7305/1,25=0,5844 H

F^/_и5=М_и5/l_О2Е=0,08254/0,86=0,09598 H

Все силы переносим в одноименную точку плана скоростей без изменения ее направления. В точке b плана скоростей прикладываем неизвестную уравновешивающую силу F_y.

Записываем уравнение моментов сил относительно полюса плана скоростей:

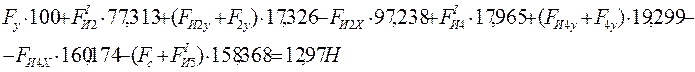
Зная величину F_y, найдем уравновешивающий момент M^/ _y

M^/ _y=F_y×l_AB=12,884*0,25=3,221 Н×м

Отклонение найденного с помощью рычага Жуковского значения момента M^/ _y  от определенного выше аналитическим методом определится:

это меньше допускаемого для инженерных расчетов значения