Силовой анализ механизма стана холодной калибровки труб

элементарной массой dm, следует приложить элементарную силу инерции

, где  – ускорение массы dm. Так как звено имеет множество точек, то и сил инерции, действующих на звено, - множество. На практике при расчете самого звена на прочность ограничиваются конечным числом сил инерции, которые сосредоточивают в центрах тяжести. В дальнейшем эти силы приводят к центру масс S звена. В результате на центр масс звена действует результирующая сила инерции

и главный момент сил инерции звена (момент пары сил инерции) . Сила инерции  и момент пары сил инерции  определяются по формулам соответственно:

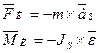
где m – масса звена;  – вектор ускорения центра масс; J_s – момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения;  - угловое ускорение звена. Знак минус показывает, что сила и момент инерции направлены противоположно ускорению.

Находим для исследуемого механизма угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат. Для начального звена в расчётном положении (см. (4.5))соответственно будем иметь

a_S1 = 0, ε₁ = -1,763 1/c².

Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающими их с аналогами скоростей и ускорений, которые имеют следующий вид:

                                                                                            (5.1)

Ускорение центра масс и угловое ускорение, например, второго звена, в соответствии с последними формулами (5.1), определится:

Результаты расчета ускорений других звеньев для расчетного положения механизма по формулам (5.1) приведены в таблице 5.1.

                                                                                                                 Таблица 5.1

Определив ускорения звеньев, находим величины моментов и сил инерции звеньев механизма:

→ для звена 1      F_И1 = 0 (Н)

М_И1 = − I_S1ε₁ = 0∙(-1,763) = 0 (Н∙м)

→ для звена 2      F_И2x = - m₂ а_S2x = -18∙(-6,628) = 119,304 (H)

F_И2y = - m₂ а_S2y = -18∙(-6,221) = 111,978 (H)

М_И2 = - I_S2e₂ = -0,13∙16,651 = -2,165 (H×м)

→ для звена 3      F_И3x = - m₃ а_S3x = -110∙(-1,215) = 133,65 (H)

F_И3y = - m₃ а_S3y = -110∙(-2,365) = 260,15 (H)

М_И3 = - I_S3e₃ = -0,33∙6,040 = -1,993 (H∙м)

→ для звена 5      F_И5x = 0 (Н)

F_И5y = - m₅ а_S5y = 1400∙(-0,211) = -295,4 (H)

М_И5 = 0 (Н∙м)

5.1.2 Силы, действующие на механизм

Для удобства дальнейшей работы в таблице 5.2 сведены все действующие на механизм силы и моменты в проекциях на оси координат со своими знаками.

Таблица 5.2

Так как направления сил и моментов учтены их знаками, то на расчетных схемах все силы изображаем в направлении координатных осей, а моменты - против хода часовой стрелки.

5.2. Определение уравновешивающего момента и реакций в кинематических парах  аналитическим методом

Силовой анализ механизма аналитическим методом проводят последовательно и отдельно для каждой структурной группы, начиная с той, в которую входит выходное звено. Начальное звено анализируют последним.

Для определения реакций в кинематических парах структурных групп и начального звена составляют и решают уравнения кинетостатики. Причем на первом этапе находят реакции во внешних кинематических парах, а затем во внутренних.

Рассмотрим определение сил в кинематических парах исследуемого механизма стана холодной калибровки труб.

5.2.1. Силовой анализ структурной группы 4-5

Начинаем анализ с рассмотрения структурной группы 4-5 (рис. 5.1). Прикладываем к ней с целью упрощения вычислений в проекциях на оси действующие на нее силы.

Записываем в проекциях на оси координат условия равновесия всех сил:

∑P_X=0        R_50x + R_43x = 0

∑P_Y=0        F₁ + F_5y + F_И5y + R_43y = 0                                                                   (5.2)

Находим из уравнений (5.2) R_43y, R_43x и R_50x:

R_43y = - F₁ - F_5y - F_И5y = (-25000) - (-13734) - (-295,4) = -10970,6 (Н)

R_43x = R_43y∙tg (180-φ₃) = (-10970,6)∙tg (180-171,1) = -1717,95 (H)

R_50x = - R_43x = 1717,95 (H)

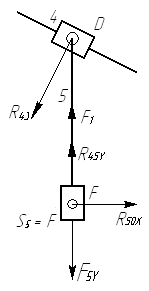рис. 5.1. Структурная группа 4-5.

5.2.2. Силовой анализ структурной группы 2-3

Помимо заданных сил и сил инерции, на группу действуют реакции R₂₁, R₃₀, R₃₄. Силы представлены через их проекции на оси координат. Проекции R_34x и R_34y найдены из анализа предыдущей группы:

R_34x = - R_43x = 1717,95 (H), R_34y = -R_43y = 10970,6 (H).

Для определения реакции в кинематических парах С и А записываем два уравнения проекций сил на координатные оси и два уравнения моментов относительно точки В для звеньев 2 и 3:

                                                               (5.3)

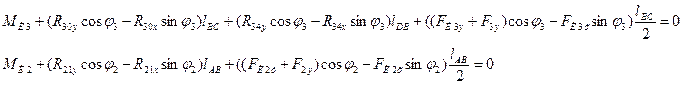
Все известные величины переносим в правые части уравнений (5.3). В результате:

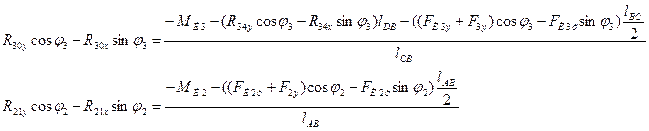
Дальнейший расчет ведем с помощью программы "MathCAD", и в результате чего:

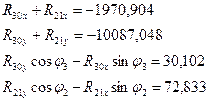                                                                                 (5.4)

Решая систему уравнений (5.4) и учитывая, что φ₂ = 73,1⁰, φ₃ = 171,1⁰, получим:

R_30x = 2914,8 (H)

R_30y = 5743,2 (H)

R_21x = -4885,7 (H)

R_21y = -6830,3 (H)

Реакции R₂₁ и R₃₀ определяться соответственно:

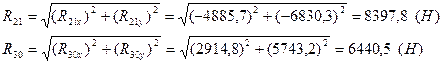
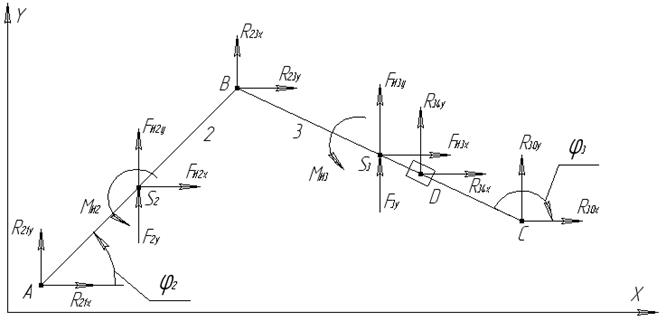
  рис 5.2. Структурная группа 2-3

Реакцию R₂₃, действующую в кинематической паре В, находим из уравнения