




1. СТРУКТУРНЫЙ АНАЛИЗ
Исследование механизма грохота начнем со структурного анализа, который предусматривает определение, описание и классификацию кинематических пар, подвижных звеньев, кинематических цепей и механизмов.
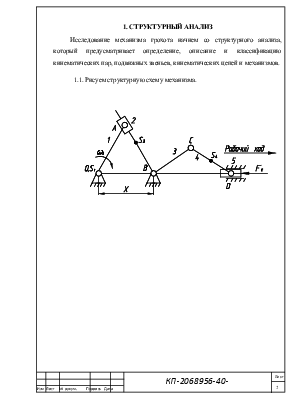
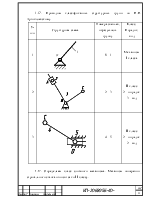
1.1.Рисуем структурную схему механизма.
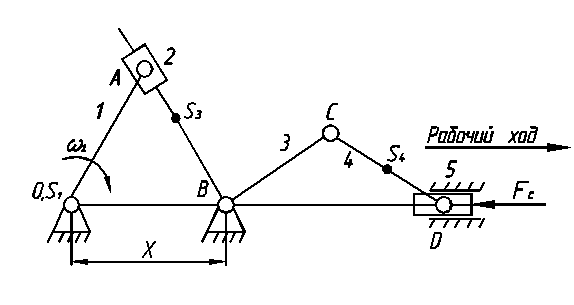
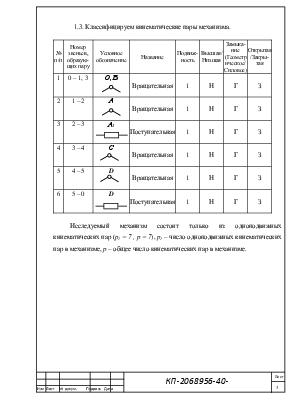
1.3. Классифицируем кинематические пары механизма.
|
№ п/п |
Номер звеньев, образую-щих пару |
Условное обозначение |
Название |
Подвиж-ность |
Высшая/ Низшая |
Замыка-ние (Геометрическое/ Силовое) |
Открытая/Закры-тая |
|||
|
|
0 – 1, 3 |
О, В
|
Вращательная |
1 |
Н |
Г |
З |
|||
|
|
1 – 2 |
А
|
Вращательная |
1 |
Н |
Г |
З |
|||
|
3 |
2 – 3 |
А3
|
Поступательная |
1 |
Н |
Г |
З |
|||
|
4 |
3 – 4 |
С
|
Вращательная |
1 |
Н |
Г |
З |
|||
|
|
4 – 5 |
D
|
Вращательная |
1 |
Н |
Г |
З |
|||
|
6 |
5 – 0 |
D
|
Поступательная |
1 |
Н |
Г |
З |
Исследуемый механизм состоит только из одноподвижных кинематических пар (р1 = 7 , р = 7), р1 – число одноподвижных кинематических пар в механизме, р – общее число кинематических пар в механизме.
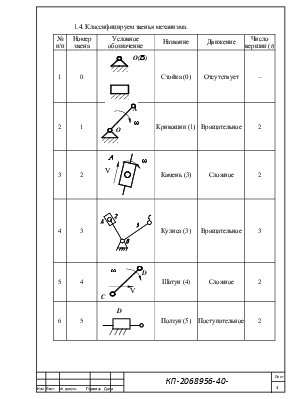
1.4. Классифицируем звенья механизма.
|
№ п/п |
Номер звена |
Условное обозначение |
Название |
Движение |
Число вершин (t) |
|||||||||||||||||||
|
1 |
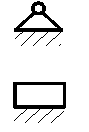
0 |
|
Стойка (0) |
Отсутствует |
– |
|||||||||||||||||||
|
2 |
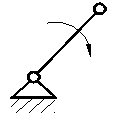
1 |
|
Кривошип (1) |
Вращательное |
2 |
|||||||||||||||||||
|
3 |
2 |
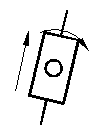
|
Камень (3) |
Сложное |
2 |
|||||||||||||||||||
|
4 |
3 |
|
Кулиса (3) |
Вращательное |
3 |
|||||||||||||||||||
|
5 |
4 |
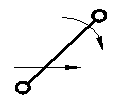
|
Шатун (4) |
Сложное |
2 |
|||||||||||||||||||
|
|
5 |
|
Ползун (5) |
Поступательное |
2 |
|||||||||||||||||||
Механизм имеет: четыре (п2 = 4) двухвершинных (t = 2) линейных звена 1, 2, 4, 5; одно (п3 = 1) трехвершинное (t = 3) звено, которое является базовым (Т=3); пять (п = 5) подвижных звеньев.
1.5. Находим число присоединений подвижных звеньев к стойке. Исследуемый механизм грохота имеет три (S = 3) присоединения к стойке.
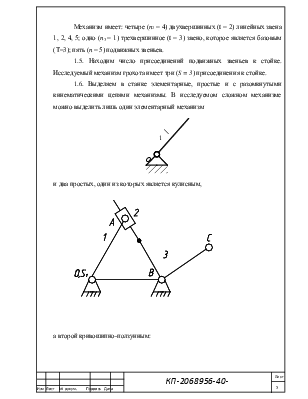
1.6. Выделяем в станке элементарные, простые и с разомкнутыми кинематическими цепями механизмы. В исследуемом сложном механизме можно выделить лишь один элементарный механизм
![]()
|
|
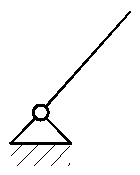
и два простых, один из которых является кулисным,
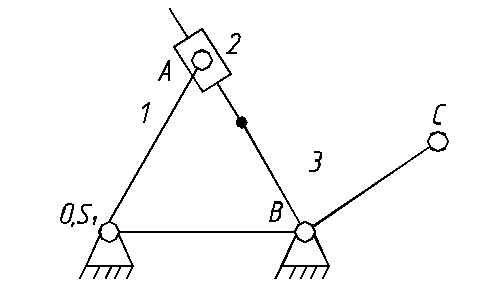
а второй кривошипно-ползунным:
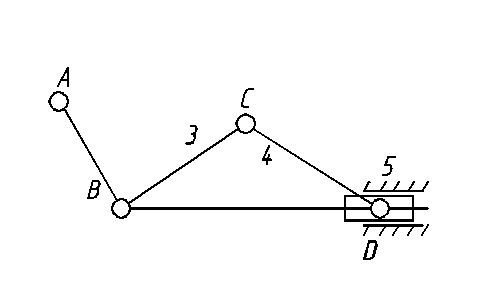
Механизмов с разомкнутыми кинематическими цепями в исследуемом станке нет.
1.7. Выявляем простые стационарные и подвижные механизмы. Станок имеет в своем составе только простые стационарные механизмы.
1.8. Находим звенья закрепления и присоединения. В исследуемом сложном механизме звеньев закрепления нет. У него есть только одно звено присоединения – звено 3 (кулиса). Звено 3 одновременно входит в два простых механизма –кулисный и кривошипно-ползунный. Значит для этого звена К3 = 2.
1.9. Классифицируем механизм станка. Исследуемый механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеют в своем составе только замкнутые кинематические цепи.
1.10. Определяем подвижность простых механизмов. Анализируя движение звеньев механизма и элементов кинематических пар можно установить, что исследуемый механизм и простые механизмы, входящие в его состав существуют в трехподвижном (П = 3) пространстве, в котором разрешены следующие простейшие независимые движения: два поступательных х и у вдоль соответствующих осей; одно вращательное jZ вокруг оси Z.
Формулы для определения подвижности этих механизмов примут вид соответственно:
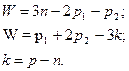
Определим
подвижность (W![]() ) кулисного
механизма. Этот механизм имеет: три (n = 3) подвижных звена 1, 2, 3;
четыре (p = p
) кулисного
механизма. Этот механизм имеет: три (n = 3) подвижных звена 1, 2, 3;
четыре (p = p![]() = 4)
одноподвижные кинематические пары О, А, В, С. Тогда подвижность определится:
= 4)
одноподвижные кинематические пары О, А, В, С. Тогда подвижность определится:
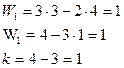
Найдем
подвижность (W2)
кривошипно-ползунного механизма. Этот механизм имеет: (n = 3) подвижных звена 3,
4, 5 и четыре (p = p![]() = 4) кинематические
пары А, В, С, D. Так как
кривошипно-ползунный механизм по количественному и качественному составу
кинематических пар и звеньев ничем не отличается от кулисного, то его
подвижность определяется по тем же формулам и также равна единице (W2 = 1).
= 4) кинематические
пары А, В, С, D. Так как
кривошипно-ползунный механизм по количественному и качественному составу
кинематических пар и звеньев ничем не отличается от кулисного, то его
подвижность определяется по тем же формулам и также равна единице (W2 = 1).
1.11. Определяем подвижность сложного механизма. Подвижность сложного механизма грохота определяется по формуле
![]() .
.
имеем, что
![]()
Теперь подвижность сложного механизма определим по формуле Чебышева:
![]()
Полученные результаты совпадают.
1.12. Проведем анализ структурной модели механизма и проверим, соответствует ли исследуемый механизм структурной математической модели. Механизм имеет: семь (р = 7) одноподвижных (р1 = 7) кинематических пар; пять (п = 5) подвижных звеньев, из которых одно (п3 = 1) базовое (T = 3) трехвершинное (t = 3) и четыре (п2 = 4) двухвершиных (t = 2); три присоединения к стойке (S = 3) и нет звеньев закрепления (Z = 0).
Подставив эти исходные данные в структурную математическую модель, получим:
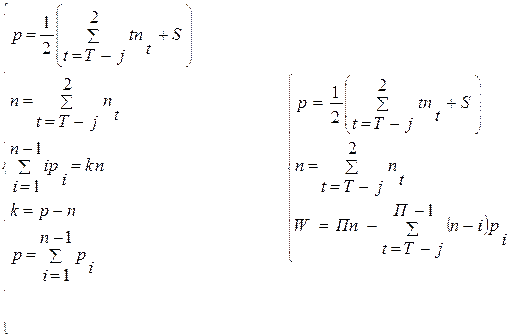
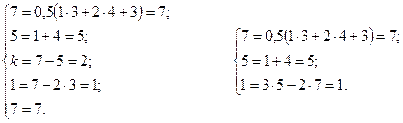
Так как уравнения превратились в тождества, то исследуемое устройство имеет правильную структуру и является механизмом.
1.13 Выделяем в исследуемом устройстве механизм 1класса, который в соответствии с классификацией И.И. Артоболевского механизм 1 класса для исследуемого механизма совпадает с элементарным механизмом.
1.14. Выделяем структурные группы Ассура. В механизме грохота можно выделить следующие структурные группы:
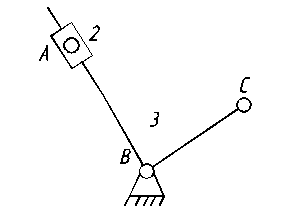
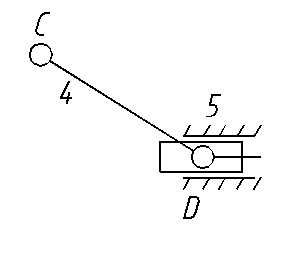
Выделенные структурные группы полностью подобны по видовому и количественному составу звеньев и кинематических пар. Каждая из структурных групп имеет: два подвижных звена (n/ = n2/ = 2), причем все звенья двухвершинные (t = 2) и, значит, базовое звено также имеет две вершины (Т = 2); три (p = p1 = 3) одноподвижные кинематические пары, из которых две внешние (S/ = 2).
1.15. Проверим, соответствуют ли выделенные структурные группы их математическим моделям. Группы структурно подобны, поэтому проверку ведем только по одной группе CDО. Подставив в структурную модель группы их исходные данные, получим:
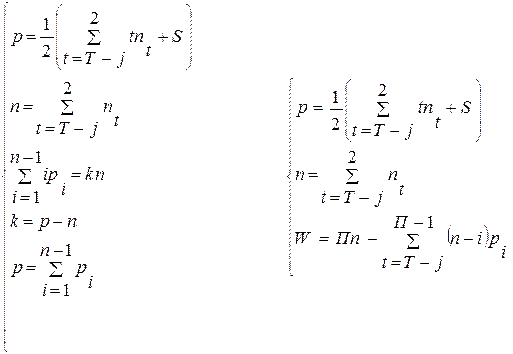
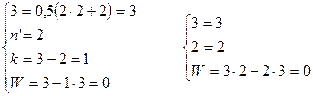
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.