4. Силовой анализ механизма.
Силовой анализ будем проводить как аналитическим, так и графическим методами по следующему алгоритму:
определим силы инерции звеньев
1. выделяем структурные группы Ассура
2. начиная с последней структурной группы, в которую входит начальное звено, последовательно определим реакции во всех кинематических парах;
3. из условия равновесия начального звена найдем уравновешивающий момент и реакцию, действующую на него со стороны стойки.
4.1. Определение сил инерции звеньев.
Согласно принципу Даламбера звено механизма можно рассматривать как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции.
Сила инерции Fи и момент пары сил инерции Ми можно определить по следующим формулам:
FИ=-mias
МИ=-Isei
Где m- масса звена, аs- вектор ускорения центра масс, Js- момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения, e- угловое ускорение звена.
Находим для исследуемого механизма угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.
Для начального звена в первом положении будет:
аs1=0; e1=-3,0748 1/с2; w1=6,0716 1/с
Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающим их с аналогами скоростей и ускорений, которые имеют следующий вид:
аSix=Six''w12+ Six'e1; аSiy=Siy''w12+ Siy'e1 (3.1)
ei=ji''w12+ ji'e1
Ускорение центра масс и угловое ускорение для второго звена примут вид:
аS2x=(-0.28)·6.07162+(-0.062)·(-3,0748)=-10,144 м/с2
аS2y=(-0.023)·6.07162+(-0.056)·(-3,0748)=-0,698 м/с2
e2=0,685·6.07162+0.516·(-3,0748)=23,6991/с2
аS4x=(-0,426)·6.07162+(-0.168)·(-3,0748)=-15,22 м/с2
аS4y=(0.032)·6.07162+(-0,0026)·(-3,0748)=1,216 м/с2
e4=0.11·6.07162+(-0,002)·(-3,0748)=4,105 1/с2
аS5x=(-0,223)·6.07162+(-0,168)·(-3,0748)=-7,738 м/с2
e3=0,683·6.07162+0,43·(-3,0748)=23,87 1/с2
Определив ускорения звеньев, находим главный вектор и главный момент сил инерции звеньев механизма:
Звено 1: Fи1=0 H;
Mи1=-Io1e1=-1.1·(-3.0748)=3.382 H;
Звено 2: Fи2х=-m2·аS2x=-18·(-10.144)=182.605 H;
Fи2y=-m2·аS2y=-18·(-0.698)=12.56 H;
Mи2=-Is2·e2=-0,6·23.699=-14.2195 H·м;
Звено 3: Fи3y=0 H;
Fи3x=0 H;
Mи3=-Is3·e3=-1.1·23.87=-26.2619 H·м;
Звено 4: Fи4x =-m4·аS4x=-100·(-15.22)=1522.26 H;
Fи4y=-m4·аS4y=-100·1.216=-121.605H;
Mи4=-Is4·e4=-42·4.105=-172.432 H·м;
Звено 5: Fи5x =-m5·аS5x=-500·(-7.738)=3869.005 H;
Fи5y=0 H;
Mи4=0 H;
|
Силы инерции |
Cилы тяжести |
Сила сопр. |
||||||||||
|
Mи1 |
Fи2х |
Fи2y |
Mи2 |
Mи3 |
Fи4x |
Fи4y |
Mи4 |
Fи5x |
F2y |
F4y |
F5y |
Fc |
|
-3.382 |
182.605 |
12.56 |
-14.2195 |
-26.261 |
1522.26 |
-121.6 |
-172.58 |
3869.005 |
-176,6 |
-981 |
-4410 |
-3800 |
4.2. Силовой расчет последней присоединенной группы Ассура.
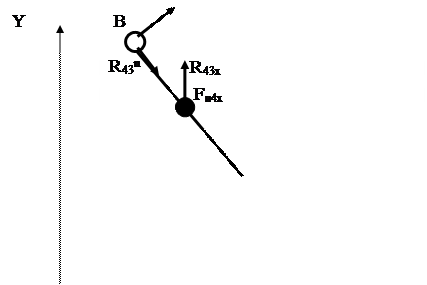
Рассмотрим структурную группу 4-5 .Прикладываем к ней в проекциях на оси, действующие на нее силы. Действие на звено 5 со стороны стойки заменяем реакцией R5d, а на звено 4 со стороны звена 3 реакцией R43.
Записываем в проекциях на оси координат условия равновесия всех сил, действующих на звено 5:
åFX=0
R43n·cos(180-j4)+R43t ·sin(180-j4)+ Fи4x+Fи5x+Fc2=0
åFY=0
R43t·cos(180-j4)+ R43n ·sin(180-j4)+ Fи4y+G4+G5+R50 =0 (3.2)
åMd=0
-R43t·L4+Mи4-Fи4х·L4·0,5·sin(180-j4)-(G4+Fи4y)·(L4/2)·cos(180-j4)=0
R43t
![]()
![]()
![]()
|
![]()
![]() Fи5x
Fи5x
![]()
![]()
![]()
![]()
![]() Fc2
Fc2
|
||||||||
|
||||||||
|
||||||||
Решая уравнение (3.2), получим:
R43t=(Mи4/L4)-0,5·Fи4х·sin(180-j4)-0,5·(Fи4y+G4)·cos(180-j4)=-124.15H
R43n=(-R43t·sin(180-j4)+Fи4x+Fc2+Fи5x)/cos(180-j4)=-10541.28 H
R50=-[ R43t·cos(180-j4)+R43n·sin(180-j4)+Fи4х+G4+G5]=11385.48 H
R43x= R43t·sin(180-j4) +R43n·cos(180-j4)=-9191.25 H
R43y= R43t·cos(180-j4) +R43n·sin(180-j4)=-5377.87 H
R43=![]() =10649 H
=10649 H
Реакция R34 является внутренней, она равна по модулю и противоположна по направлению внешней реакции R43 и поэтому : R34= -R43.
Для исследуемого положения реакции определятся:
R34=-10649Н R43= 10649 Н R50=11385.48 H
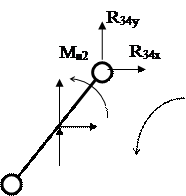
4.3. Силовой расчет первой присоединенной группы Ассура (структурной группы 2-3).
Помимо заданных сил и сил инерции, на группу действуют реакции R34 ,R30 R21. Силы представлены через их проекции на оси координат.
Проекции R34х и R34y были найдены из анализа предыдущей группы.
Для определения реакции в кинематических парах А и С записываем два уравнения проекций на координатные оси и два уравнения моментов относительно точки В:
åМB(3)=Mи3-R30t·Lbc+G3·cos(180°-j3)·Lbc=0
åМB(2)=Mи2-R21t·Lab+(G3+Fи2y)·Lab·0,5·sin(j2-90°)·Lbc+Fи2х·Lab·0,5·
·cos(j2-90°)=0
åFx=R34x+Fи2x+R21t·cos(j2-90°)-R21n·sin(j2-90°)-R30t·sin(180-j3)-R30n·cos(180-j3)=0
åFy= R34y+Fи2y+G2+G3+ R21t·sin(j2-90°)+R21n·cos(j2-90°)-R30t·cos(180-j3)+R30n·sin(180-j3)=0
 |
|||||
|
|
 B
B
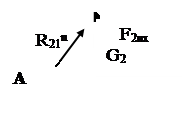 |
|||
|
|
|
G2
Решив уравнения, получим:
R30t =(Mи3/Lab)+G3·cos(j2-90°)=-69.427 H
R21t=(Mи2/Lоа)+(G2+Fи2y)·0,5·sin(j2-90°)+Fи2х·0,5·cos
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.