Физика \ Радиофизика

Резонатор как элемент СВЧ цепи, страница 3

Коэффициент связи мы ввели как . Коэффициент отражения на частоте резонанса (при ) равен  - вещественное число , а в широкой полосе частот вокруг резонанса  - комплексное число: ;   - эта величина равна напряжению на эквивалентном сечении резонатора, нормированному на амплитуду напряжения падающей волны. В то же время . Посмотрим теперь, как выглядит на комплексной плоскости геометрическое место точек, соответствующих этому вектору нормированного напряжения на резонаторе (годограф). Назовем вектором A нормированное напряжение на любой частоте в окрестности резонанса, а вектором B на резонансной частоте: , . Алгебраическим преобразованием последнего уравнения к виду  получаем уравнение для суммы векторов: . Ввиду  наличия мнимой единицы во втором слагаемом слева, два эти вектора образуют прямой угол, а гипотенуза этого треугольника постоянна - вектор B – это нормированная амплитуда в точке резонанса. Вершины всех возможных прямых углов, опирающихся на постоянный отрезок, образуют окружность - с этим постоянным отрезком в качестве диаметра, как показано на рисунке.

Эту окружность можно поместить прямо на круговую диаграмму сопротивлений.  - для эквивалентного сечения представления параллельным контуром, 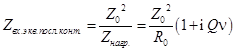 - в сечении эквивалентного представления последовательным контуром, на расстоянии четверть волны от параллельного представления по длине линии. Когда мы начнем удаляться от сечения включения резонатора вдоль длинной однородной линии передачи, каждая точка этой окружности, соответствующая фиксированному импедансу нагрузки, будет перемещаться вместе с фазой отраженной волны по окружности вокруг центра круговой диаграммы. При удлинении линии на  точка короткого замыкания, соответствующая бесконечной расстройке, перекатится в точку холостого хода, и картина зависимости импеданса от расстройки станет соответствовать резонансу последовательного соединения емкости и индуктивности. При любой длине линии от точки наблюдения до резонатора, напряжение и фаза напряжения в точке наблюдения будет изображаться вектором от точки К.З. до точки на окружности резонанса, нормированным на вектор амплитуды падающей волны – ему соответствует постоянный вектор от точки К.З. до центра диаграммы – точки согласования. Это просто в точности соответствует обычному закону преобразования импеданса в длинной линии без потерь 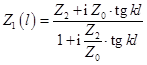. Коэффициент отражения 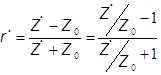, где Z0 - волновое сопротивление линии передачи. Коэффициент стоячей волны напряжения (тока) . Коэффициент связи резонатора  , где . При этом КСВН или  . На экранах современных векторных анализаторов цепей резонансы обнаруживаются как характерные завитки амплитудно-фазовой характеристики.


[1] Эта простейшая теоретическая идеализация  хорошо работает в СВЧ диапазоне, но с ростом частоты уменьшается толщина скин-слоя и, соответственно, возрастает его сопротивление. В оптическом диапазоне уже появляются дополнительные особенности - медь, например, не идеально серебристая, а красная, золото желтое...А для жесткого рентгеновского излучения металл вообще уже довольно прозрачен.   Поэтому  начиная с некоторой частоты заметные резонансы, как таковые, исчезают

Скачать файл