Коэффициентом связи "![]() " называется отношение потерь вне
резонатора к потерям в резонаторе:
" называется отношение потерь вне
резонатора к потерям в резонаторе: ![]() - и, таким образом, по сути, это нормированное
к волновому сопротивлению линии сопротивление потерь эквивалентного контура.
Связь, когда
- и, таким образом, по сути, это нормированное
к волновому сопротивлению линии сопротивление потерь эквивалентного контура.
Связь, когда ![]() , соответствует идеальному (без отражения)
согласованию линии и резонатора, и называется критической. При этом
нагруженная добротность ровно в два раза меньше собственной:
, соответствует идеальному (без отражения)
согласованию линии и резонатора, и называется критической. При этом
нагруженная добротность ровно в два раза меньше собственной: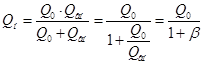 .
.
Резонатору сопоставляются параметры эквивалентного контура путем анализа частотных свойств коэффициента отражения от него в линии.
В теории радиочастотных цепей частотные свойства
параллельного колебательного контура принято описывать функциями расстройки ![]() : полное (комплексное) сопротивление -
импеданс - контура
: полное (комплексное) сопротивление -
импеданс - контура ![]() ; полную проводимость
; полную проводимость ![]() .
.
Измерить напряжения и токи в СВЧ диапазоне невозможно,
но довольно просто измерить мощность ![]() , поглощенную в резонаторе. Поглощенная
мощность зависит от расстройки:
, поглощенную в резонаторе. Поглощенная
мощность зависит от расстройки:
|
|
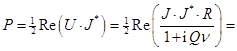
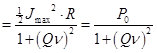 , где
, где ![]() - мощность, поглощаемая на резонансной
частоте. Поэтому измеряют отношение мощности, поглощаемой на разных частотах, к
мощности, поглощаемой при резонансе. Ширина полосы резонанса определяется из
графика зависимости поглощаемой мощности от частоты по точкам половинной
мощности. Обозначив через
- мощность, поглощаемая на резонансной
частоте. Поэтому измеряют отношение мощности, поглощаемой на разных частотах, к
мощности, поглощаемой при резонансе. Ширина полосы резонанса определяется из
графика зависимости поглощаемой мощности от частоты по точкам половинной
мощности. Обозначив через ![]() обобщенную расстройку -произведение
добротности на расстройку мы должны получить график, приведенный на рисунке2.
(Если же форма кривой окажется отличной от данной, скорее всего это будет
означать, что возбуждается не один резонанс, а два или более связанных между
собой резонансов с близкими собственными частотами.) Диапазон частот
обобщенную расстройку -произведение
добротности на расстройку мы должны получить график, приведенный на рисунке2.
(Если же форма кривой окажется отличной от данной, скорее всего это будет
означать, что возбуждается не один резонанс, а два или более связанных между
собой резонансов с близкими собственными частотами.) Диапазон частот ![]() , соответствующий диапазону обобщенной
расстройки
, соответствующий диапазону обобщенной
расстройки ![]() (где поглощение более половины максимальной
мощности, а напряжение на контуре не менее
(где поглощение более половины максимальной
мощности, а напряжение на контуре не менее ![]() от максимального), называется полосой
резонанса. Таким образом, возникают следующие соотношения:
от максимального), называется полосой
резонанса. Таким образом, возникают следующие соотношения:
![]() ;
; ![]() . Отсюда важнейшая формула для определения
добротности по результатам частотных измерений:
. Отсюда важнейшая формула для определения
добротности по результатам частотных измерений: ![]() - добротность равна частоте резонанса,
деленной на ширину полосы резонанса. Этим способом измерения добротности
можно пользоваться при не слишком малых (должен быть явный резонанс) и не
слишком больших величинах добротности. (Добротность сверхпроводящих резонаторов
достигает десятков миллиардов при собственной частоте в единицы гигагерц, и
измерить полосу вообще невозможно, так как слишком велика нестабильность
резонансной частоты из-за деформаций резонатора за время измерений - в таких
случаях проще измерить постоянную времени затухания колебаний после мгновенного
отключения возбуждения.)
- добротность равна частоте резонанса,
деленной на ширину полосы резонанса. Этим способом измерения добротности
можно пользоваться при не слишком малых (должен быть явный резонанс) и не
слишком больших величинах добротности. (Добротность сверхпроводящих резонаторов
достигает десятков миллиардов при собственной частоте в единицы гигагерц, и
измерить полосу вообще невозможно, так как слишком велика нестабильность
резонансной частоты из-за деформаций резонатора за время измерений - в таких
случаях проще измерить постоянную времени затухания колебаний после мгновенного
отключения возбуждения.)
|
От изолированного
абстрактного колебательного контура вернемся теперь к резонатору,
являющемуся нагрузкой линии передачи с фиксированным коэффициентом связи |
Проводимость контура G ![]() , полная проводимость вблизи резонанса
, полная проводимость вблизи резонанса ![]()
![]() . Коэффициент отражения обусловлен
относительной величиной проводимости нагрузки и волновой проводимости линии
передачи:
. Коэффициент отражения обусловлен
относительной величиной проводимости нагрузки и волновой проводимости линии
передачи:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.