Клистрон. Отражательный клистрон. Модуляция по скорости. Группировка в пространстве дрейфа

Клистрон. Отражательный клистрон

Модуляция по скорости

Электроны проходят  через зазор группирующего резонатора постоянным непрерывным потоком со скоростью и энергией, обусловленной ускоряющим напряжением U₀ электронной пушки

В группирующем резонаторе они слегка подгоняются или притормаживаются силой высокочастотного электрического поля - в зависимости от фазы напряжения U₁  на зазоре шириной d:

Для интегрирования этого уравнения движения обозначим начальные условия в момент влета 

    ,   где - момент влета. Интегрируя уравнение движения от t₁ до t имеем

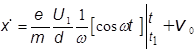
Введем т.н. угол пролета , характеризующий относительное время пребывания электрона в резонаторе по отношению к периоду ВЧ колебания в нем. Для дальнейшего определения зависимости скорости электрона на выходе из группирующего резонатора от времени его влета, сначала умножим и разделим выражение скорости на U₀. Тогда:

.

Используя тригонометрическое тождество  , перепишем выражение скорости в другой форме:

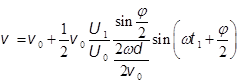
Далее, обозначим .  Обычно , т.е.модуляция скорости мала. Поэтому можно считать, что длительность полета электрона в зазоре определяется только величиной U₀, и  использовать невозмущенный угол пролета: .  Обозначим через длительность пролета зазора, а отсчет времени (для удобства в дальнейшем) условимся начинать от середины зазора группирующего резонатора:   , и . Знак штриха при времени далее за ненадобностью опустим.

После этого формула модулированной скорости электронов имеет вид: 

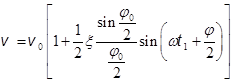
Введем для параметра эффективности модуляции обозначение 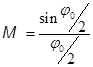 , и формула скорости примет окончательный вид:

 .               (1)

Величина  имеет смысл амплитуды модуляции скорости. Очевидно, что чем больше эффективность М, тем меньше потребуется величина напряжения U₁  для получения той же модуляции, т.е. меньше мощности потребуется для раскачки группирующего резонатора на вход клистрона – увеличится его коэффициент усиления.  При , как это обычно и бывает, энергия электромагнитного поля на ускорение электронов не тратится, т.к. сколько одни электроны энергии забирают, ускоряясь, столько же другие отдают, притормаживаясь. Таким образом, энергия входного сигнала тратится только на омические потери в стенках резонатора. (Как в ламповом каскаде с общим катодом). Наиболее рационален малый зазор  , но возможность уменьшения зазора при фиксированной величине U₁ ограничена электрической прочностью. Практически в клистронах , что соответсвует величине эффективности модуляции 0,6<М<0,9. Если продолжительность движения электрона в зазоре группирующего резонатора кратна частоте модуляции, т.е j= 2p, 4p … , то М=0, т.к. каждый электрон полпериода ускоряется, и столько же времени тормозится.

Группировка в пространстве дрейфа

После группирующего резонатора поток электронов попадает в т.н. пространство дрейфа длиной . Длина его  достаточно велика, чтобы электроны за счет разности скоростей собрались в группы, и пучек из непрерывного потока, таким образом, превратился в последовательность следующих друг за другом сгустков, проходящих через зазор выходного резонатора. Пространство дрейфа представляет собой трубку достаточно малого диаметра, чтобы волны рабочей частоты не могли по ней распространятся – т.е. для них эта трубка  должна быть закритическим волноводом. Для простоты полагаем, что высокочастотные поля в пространстве дрейфа вообще отсутствуют. Пучок по пространству дрейфа движется вдоль внешнего магнитного поля от фокусрующих магнитов, удерживающих пучек от поперечного расширения, продольным же электричеким отталкиванием электронов от объемного заряда сгустков тоже пренебрегаем, полагая поле объемного заряда сгустков относительно небольшим.

Отсчет времени ведем от середины зазора модулирующего (группирующего) резонатора.

Электроны преодолевают путь   между серединами резонаторов за разное время со скоростью (1):

                   (2)

Умножив это уравнение на  и поделив на , вводим т.н. угол пролета в дрейфовом пространстве

Электрон, пересекший середину зазора 1 в момент времени  , достигнет середины зазора выходного резонатора 2 в момент времени , где - длина пространства дрейфа: . При и  это приблизительно

.

Обозначив угол пролета в дрейфовом пространстве , и введя   - параметр группировки, имеем

; .                  (3)

Если Х=0, то фаза влета во второй резонатор линейно зависит от фазы вылета из первого, и  группировки нет. Эти соотношения иллюстрируются на Рис.1 а) – графики движения отдельных групп электронов, б) – график времени прибытия электронов в выходной резонатор от времени убытия из группирующего резонатора.

Вычислим ток во втором зазоре (), как функцию тока в первом ().

По закону сохранения электрического заряда (пренебрегаем только ничтожными потерями электронов на стенках) для каждой конкретной (очень короткой) группы электронов можно написать уравнение равенства переносимого ими заряда через первый и второй зазор: , где    и  - продолжительность прохождения промежутков этой группой, т.е. промежутки времени между прохождением зазоров первым и последним электроном выделенной группы. (Данное уравнение записано со знаками абсолютной величины, т.к. из-за разности скоростей, приобретенной в группирующем резонаторе, головной и хвостовой электроны выбранной группы за время дрейфа могут поменяться местами.) В первом зазоре ток еще постоянный  – он совсем не модулирован, т.к. пучок не успел сгруппироваться  по плотности. А для тока во втором зазоре мы можем теперь написать выражение

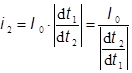.                 (4)

Но в пределе бесконечно коротких интервалов времени  скорость всех электронов в выбранной группе можно считать совершенно одинаковой, поэтому время, за которое группа электронов проскакивает всякие зазоры, обратно пропорционально ее скорости, и для отношения интервалов времени можно воспользоваться ранее полученной формулой модуляции скорости:

, и тогда получится (весьма приблизительное[1]) выражение для тока в зазоре выходного резонатора  

.                              (5)

Как видим, эта формула дает весьма нереалистичную величину беконечного тока при параметре группировки, прибижающимся к единице и далее. Картину можно регуляризовать, «размазав» ток в виде непрерывного распределения плотности тока, так чтобы обрела точный смысл операция суммирования числа одновременно прибывающих в выходной резонатор электронов. На Рис. 2 представлена картинка, полученная численным вычислением с использованием Гауссова размытия линии графика тока.