Согласующие волноводные переходы. Симметричные переходы

Согласующие волноводные переходы

Для согласования нагрузок, импеданс которых сильно отличается от волнового сопротивления линии  передачи (или оптимального сопротивления нагрузки для генератора),  применяются плавные (экспоненциальные) и ступенчатые (биномиальные и Чебышевские) трансформирующие переходы. Технологически проще в изготовлении переходы ступенчатые, и для них существуют методы расчета, обеспечивающие получение заданных частотных характеристик. Наиболее широкополосное согласование при указанном наибольшим уровне отражения и с минимальным числом промежуточных ступеней обеспечивают Чебышевские переходы. В их расчете используется свойство полиномов Чебышева, описывающих в данном случае амплитуду отраженного сигнала, не превышать известную нормированную величину. При этом в полосе согласование имеется несколько нулей отражения - столько, сколько промежуточных волноводных линий использовано в переходе. Биномиальные же переходы обеспечивают наибольшую гладкость коэффициента отражения, но их частотная полоса согласования при тех же габаритах меньше. Простейший ступенчатый согласующий переход - четвертьволновый трансформатор, с волновым сопротивлением Z_T, равным среднему геометрическому  между волновыми сопротивлениями на выходе Z₂ и входе Z₁ : . Условие согласования выполняется только на

на частоте f₀,  соответсвующей четвертьволновой длине линии . При этом условии отраженная волна приходит от второго соединения к первому в противофазе, и они полностью гасят друг друга благодаря тому, что коэффициенты отражения по модулю равны - их равенство предопределено специальным выбором волнового сопротивления вставки : . В полосе частот возле этой центральной, при сложении отражений надо учитывать угол фазы, с которой приходит отраженный от второй ступеньки сигнал к первой:. При отклонении частоты от номинальной  происходит изменение фазового угла

. Суммарное отражение оказывается очень заметным даже в полосе ±25% от номинальной частоты.

Для более широкополосного согласования  применяются протяженные – плавные (например,

экспоненциальные), или многоступенчатые переходы. В самом общем виде полное отражение от плавного перехода можно представить интегралом  отражений от бесконечно малых ступенек волнового сопротивления вдоль длины перехода.

На каждой малой ступеньке амплитуда отраженного сигнала равна

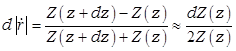
Для учета набега фазы при прохождении протяженности ступеньки туда и обратно дифференциал отражения снабжается фазовым множителем

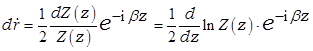                               а общее отражение дается интегралом

,   где .                                    

Для переходов с конечным числом n ступеней одинаковой (электрической) длины d получается сумма       

                                                         , где , а  - удвоенный модуль коэффициента отражения от n-й ступеньки, поделенный на длину ступеньки. Модуль коэффициента отражения от ступеньки равен

Полагая амплитуду падающей волны за единицу, для модуля амплитуды отраженной волны с помощью тождественного преобразования получаем выражение, в котором отсчет фаз отражений ведется от середины перехода:

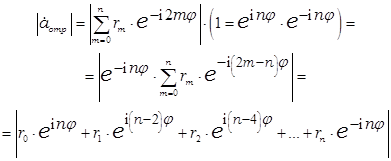
Ограничимся теперь симметричными переходами, у которых коэффициенты отражения ступеней расположены симметрично относительно середины, и попарно объединим члены суммы с одинаковым по величине отражением, чтобы воспользоваться тождеством

.                                  

Количество ступеней n может быть четным или нечетным, поэтому наибольшая величина индекса m определена может быть двумя способами:  для четного случая, и  для нечетного, при этом у центрального перехода фаза равна нулю, а фазовый множитель равен единице. Таким образом, для нечетного числа ступеней

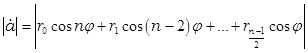                                 а для четного n

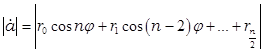
Для косинусов кратных углов имеет место формула разложения [Г.Корн и Т.Корн Справочник по математике для нучных работников и инженеров Наука М. 1974 стр 723 (21.2-13)]:

, где  - биномиальные коэффициенты. После подстановки  получается полином только от косинуса набега фазы на одной ступеньке. Обозначив  мы можем утверждать, что для абсолютной величины отражения существует представление выражением

                                                         где M – не зависящий от частоты масштабный коэффициент, а  - полином n-й степени с единичным коэффициентом при старшей степени x, причем  зависит от частоты через длину волны в линии. Таким образом, задача найти такой полином n-й степени с единичным коэффициентом при старшем члене , чтобы он имел наименьшее отклонение от 0 в заданном интервале величин аргумента «x». Зная заданную ширину потребного диапазона изменения , в котором нам хочется иметь согласование, введем новую переменную , чтобы нормировать интервал изменения  нового аргумента полинома «y» к  посредством коэффициента «t», величина которого характеризует широкополосность перехода: 

.                                          

Теперь можно переформулировать задачу – найти полиномы с единичным коэффициентом при старшем члене  с фиксированным отклонением в диапазоне [-1,1]. Такие полиномы известны, как нормированные полиномы Чебышева:

,                                                а ненормированный полином Чебышева, имеющий на интервале  отклонение не более единицы от нуля определяется через тригонометрические функции