Согласующие волноводные переходы. Симметричные переходы, страница 2

,                                               при этом между ними имеет место рекуррентное соотношение . Перечислим первые пять полиномов:

        

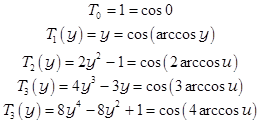
На рисунке представлены графики этих полиномов в виде фигур Лиссажу на единичном отрезке.

Как использовать этот замечательный факт?  Надо так распределить величины отражения между ступенями перехода, чтобы их сумма зависела от частоты как полином Чебышева, т.е. сделать так, чтобы общий коэффициент отражения всего перехода зависел от частоты (через набег фазы на ступеньках) как .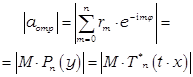

Обозначим через R_max наихудший коэффициент отражения, когда все отражения сходятся  в одной фазе – он равен отражению от одной ступеньки, если бы на ней происходил полный скачок волнового сопротивления от начального к конечному:

                                                    

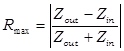
Масштабный коэффициент для n-ступенчатого перехода ( n-ого полинома) равен

                                                           и распределение коэффициентов отражения по ступеням дается в таблице для разного количества ступеней

Кол-во отражаю-щих ступеней	Кол-во вставлен-ных линий	Коэффициенты отражения от ступеней по порядку следования
1	n =0	M=Rmax
2	n =1
3	n =2
4	n =3
5	n =4

Общие формулы для произвольного числа вставочных линий [на основе Фельдштейн А.Л. Явич Л.Р. Смирнов В.П. Справочник по элементам волноводной техники «Сов. радио» М. 1968]:

1)  Для четного числа  n = 2N нечетное число отражающих порогов n +1; отражение от порога каждой  ступени по порядку следования:

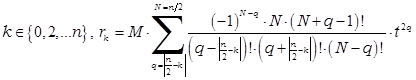
2)  Для нечетного числа n = 2N – 1 четное число отражающих порогов n +1; отражение от каждого порога по порядку следования:

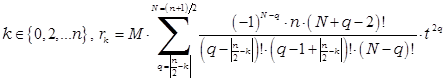
Потребное волновое сопротивление для каждой последующей ступени определяется из волнового сопротивления предыдущей по найденному коэффициенту отражения порога между ними согласно уравнению : или  - в зависимости от того, повышает или понижает трансформатор волновое сопротивление.

Пусть для примера нам дано задание рассчитать Чебышевский переход, обеспечивающий согласование прямоугольных волноводов Н₁₀ в диапазоне частот от f_min=2250 до f_max=3550 МГц с коэффициентом отражения не более r_доп<0,06 во всем этом диапазоне. Даны размеры волновода – ширина постоянная а=0.072 м, а высота меняется от b_in=0.034 м до b_out=0.1 м. Требуется определить необходимое количество,  длину и высоту промежуточных волноводов. Выполнение этой процедуры состоит из нескольких этапов.

1. Из соотношения находим величину  t:

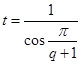                                                          где

                           

- так называемый коэффициент перекрытия диапазона. Находим его из указанных в задании величин:

.

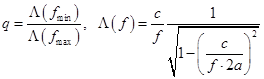Получаем q = 3.382307  и из t = 1.326509.

2. Определяем необходимое количество вставочных промежуточных волноводов перехода «n». Для этого находим необходимый коэффициент выигрыша , который следует получить благодаря  применению n – ступенчатого перехода по сравнению с самым неблагоприятным отражением «r_max»:

.

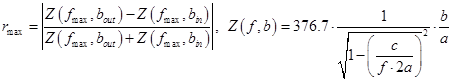Он получается r_max = 0.545455. Заданная допустимая величина отражения во всем диапазоне r_доп = 0.06. Поэтому выигрыш  = 9.090909. Для найденной в первом пункте величины t разные варианты Чебышевского перехода дают следующие величины выигрыша:   T₂(t) = 2.51925, T₃(t) = 5.357105, T₄(t) = 11.693241, последняя величина больше необходимой и, поэтому, нас удовлетворяет – переход  должен иметь пять отражающих ступеней , то есть четыре вставочных волновода.

3.. Находим распределение коэффициентов отражения по ступеням из табличных формул с нормировочным множителем :

.

4.  Определяем размеры волноводов. Длина одной ступени

                                                оказывается равной 0.040277 м. Чтобы определить высоту ступеней в общем случае нужно определить волновые сопротивления всех линий. В данном конкретном случае прямоугольного волновода постоянной ширины волновое сопротивление просто пропорционально высоте. (В случае коаксиальной линии оно пропорционально логарифму отношения диаметров внутреннего и внешнего проводников).  Кроме того, волновое сопротивление волновода зависит и от частоты, но в данном случае – когда тип волны Н₁₀, и меняется только высота b, но не ширина волновода а ,  на каждой фиксированной частоте волновые сопротивления относятся между собой как высоты волновода. Благодаря этому все рассуждения остаются в силе. Поэтому

и для нашего волновода

5. Проверка полученных результатов и построение графиков: Коэффициент отражения, вычисленный  по полиному Чебышева обозначим идеальным . Сравним его с коэффициентом отражения, «честно» вычисленным как сумма отражений с фазами