Эквивалентные четырехполюсники. Метод Вайсфлоха

Эквивалентные четырехполюсники. Метод Вайсфлоха.

Метод Вайсфлоха - это синоним "Метода смещения узла", используемого  для экспериментального определения коэффициента отражения и параметров эквивалентного четырехполюсника, соответствующего неоднородности в линии передачи. Неоднородности в волноводных линиях передач могут специально использоваться для целей согласования генератора и нагрузки, и, кроме того, настройки амплитудно-частотных характеристик ускоряющей ВЧ системы для подавления синхротронных колебаний пучка в накопительном кольце. Но, кроме того, неоднородности нежелательно возникают вследствие неидеальности конструкции или дефектов изготовления элементов ВЧ тракта. Так или иначе, для разработки СВЧ систем и анализа их работы, надо уметь сопоставлять неоднородностям эквивалентные схемы или четырехполюсники. В нашем рассмотрении будем рассматривать только идеализированные неоднородности без потерь - представимые L-C схемами без активных сопротивлений.

Для представления последовательно соединяемых элементов, каковыми являются части неразветвленного волноводного тракта, наиболее удобны цепные матрицы передачи четырехполюсников

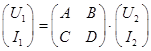                                                                                         , поскольку последовательно соединение элементов тракта отображается матричным перемножением цепных матриц, соответствующих отдельным элементам, в той же последовательности, как соединены представляемые ими элементы (матрицы в общем случае некоммутативны, так же как и влияние неоднородностей зависит от их взаиморасположения).

Рассмотрим метод измерения коэффициентов отражения от произвольной неоднородности, и особое внимание уделим правильному выбору сечений отсчета для максимального упрощения эквивалентной схемы, чтобы свести ее к идеальному трансформатору.

Однородной линии без потерь длиной l с волновым сопротивлением Z₀ соответствует цепная матрица передачи

.

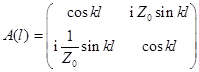Для последовательного и параллельного включения  сопротивления iX цепные матрицы имеют следующий вид:

-последовательное сопротивление не меняет ток между входом и выходом, но на нем возникает добавочное напряжение;

-параллельно подключенное сопротивление пропускает через себя ток, но не меняет напряжение между входом и выходом.

В матрицах передачи четырехполюсников без потерь элементы главной диагонали -  A и D -вещественные числа, B и C - мнимые. Величины A, B, C, D зависят от выбора сечения, и некоторым выбором сечения можно оставить ненулевыми только диагональные элементы - А и D, или B и C. Детерминант матриц, описывающих четырехполюсники без потерь,  равен единице.

Рассмотрим метод смещения узла (метод Вайсфлоха). Для исследования мы имеем неизвестную неоднородность, изображенную четырхполюсником - черным ящиком - между двух однородных линий передачи, - слева измерительная линия с зондом, для определения пучностей и узлов напряжения, ее волновое сопротивление назовем Z₀₁ - справа линия c с волновым сопротивлением Z₀₂ для подключения согласованной нагрузки Z₀₂, или измерительного короткозамыкающего шлейфа.

Первым этапом, подключим справа согласованную нагрузку, и обнаружим слева пучность (или узел) напряжения. Назовем место его расположения в линии «сечение (1)».

Падающая и отраженная волна в этих сечениях, и, следовательно, ток и напряжение между собой, строго синфазны или противофазны, т.е. импеданс является действительной величиной. Если неоднородность дает отражение с коэффициентом , то импеданс Z_вх в сечении (1), соответствующем U_max ,будет 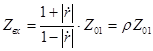, где r- КСВН.

В то же время, , а 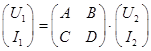. Подставив U₂=Z.₀₂ЧI₂ 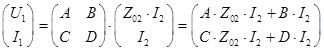и, поделив напряжение на ток, получим , но, т.к. мы уже выяснили, что  получаем уравнение

.                                              (1)

Вспомним, что A и D вещественные, а B и C - мнимые. Левая сторона уравнения вещественная. Подберем длину линии Z₀₂ так, чтобы B и C в матрице стали равными нулю, то есть, так, чтобы два отрезка линии с неоднородностью между ними предстали нам идеальным трансформатором. Для этого, вместо согласованной нагрузки поставим справа короткозамкнутый шлейф, и найдем такое сечение (2),  к.з. в котором даст нам к.з. в сечении (1). Для этой ситуации . А из уравнения (1), ввиду вещественности величин Z₀₂и Z₀₁ , следует C=0. Таким образом,  и   , а матрица передачи между этими двумя сечениями имеет вид , соответствующий идеальному трансформатору, где коэффициент трансформации напряжения 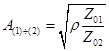, и ввиду того, что  Ясно, что четырехполюсник взаимный, и линии входа и выхода можно поменять ролями – в правую поместить измерительный зонд, а левую нагрузить согласованной нагрузкой или «заткнуть» коротко замыкающим поршнем. Тогда сечение (2) станет сечением пучности напряжения при согласованной левой линии, и все рассуждения останутся в силе..., только A и D поменяются местами. Четырехполюсник, представляющий эти две линии и неоднородность без потерь, на эквивалентной схеме можно изобразить идеальным трансформатором где коэффициент трансформации - «отношение числа витков» равно n , и .