Эквивалентные четырехполюсники. Метод Вайсфлоха, страница 2

И коэффициент трансформации, и положения сечений зависят от частоты, так что этот способ представления годен только для фиксированной длины волны. Если эквивалентная реактивность известна, то сечения (1) и (2) можно найти расчетным путем. Если нет – методом «смещения узла». Здесь наше изложение разветвляется. Рассмотрим сначала известную реактивность неоднородности, а потом вернемся к методу смещения узла.

Чтобы   найти длину линии от известной неоднородности до трансформаторного сечения путем расчета, вычислим импеданс  от последовательного  или параллельного 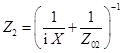  соединения неоднородности и согласованной нагрузки, и, воспользовавшись формулой трансформации импеданса линией без потерь 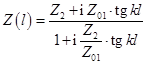, приравняем его мнимую часть нулю .  Решениями этого уравнения окажутся две величины длины l, соответствующие и пучности, и узлу напряжения, так как в них импеданс является вещественной величиной.

Для параллельного включения неоднородности эти длины равны 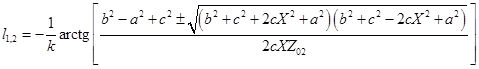, где , , .

Для последовательного

.

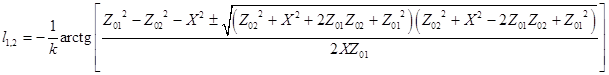В частном случае равенства волнового сопротивления линии до и после неоднородности (неоднородность в однородной линии), , все выражения для длин весьма упрощаются

,

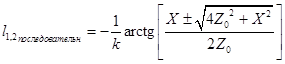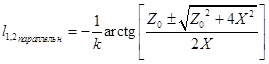. При этом величины длин соответствуют расстояниям от неоднородности до трансформаторных сечений, и матрицы передачи для разных комбинаций этих длин выглядит вот так:

;; ; . 

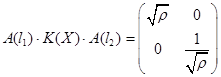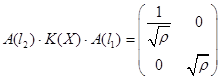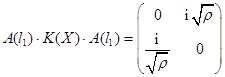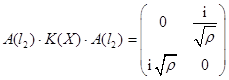Разность между длинами составляет, очевидно, l/4. Задачу о нахождении трансформаторных сечений можно решить и с помощью круговой диаграммы. Из центра, соответствующего согласованной нагрузке, реактивная добавка переносит точку в черный кружок. Эта же реактивная добавка отображает одну прямую в другую прямую, как изображено пунктирными кривыми и стрелками. Отрезок линии l₂ переводят прямую активных импедансов в одну наклонную прямую, а другую прямую отрезок линии l₁ трансформирует на линию активных импедансов.

Что касается метода Вайсфлоха, продолжим наши опыты - получив отображение к.з. справа от неоднородности в к.з. на сечении (1) слева, начнем удалять короткозамыкающий поршень в выходной (правой) линии, и следить, как вслед за ним будет двигаться сечение к.з. в линии входной (левой). Для перемещения сечения в однородной линии передачи естественной мерой пути является фазовый угол q. Замечательный факт для нас состоит в том, что сечение к.з. слева движется вслед за к.з. справа неравномерно – то отстает, то догоняет.

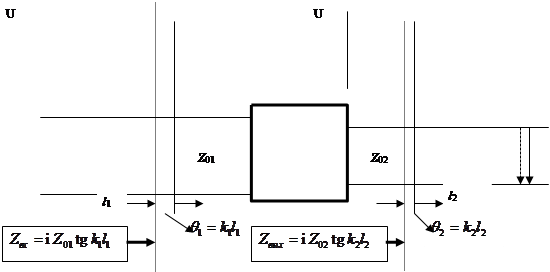Закон этого движения вполне предсказуем через трансформаторное сечение и преобразование импеданса в линии, поэтому им можно воспользоваться для установления параметров неизвестного четырехполюсника. Запишем преобразование между трансформаторными сечениями (1) и (2): . После сокращений Z и подстановки "q" это уравнение упрощается до равенства . Отсюда зависимость смещения узла "S" в левой (измерительной) линии от смещения короткозамыкающего поршня в правой имеет выражение . Вид графика этой функции зависит от коэффициента стоячей волны "r".

Точки максимумов и минимумов определяются дифференцированием кривой "S" по "q" (q₂ у нас осталась одна, индекс можно опустить…). Уравнение для экстремумов 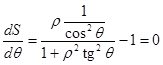 имеет решения . Этим величинам "q" соответствует максимум и минимум функции смещения узла:

.

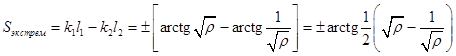Диапазон отставания и опережения узла в левой линии обозначим  . . ;.

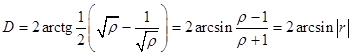Наблюдая за смещением узлов, мы с гораздо более высокой точностью можем определить положение трансформаторных сечений и коэффициент отражения (КСВН), чем при поиске пучности напряжения от согласованной нагрузки с неоднородностью. Сделать КЗ гораздо проще, чем удостовериться в согласованности нагрузки, и узел к.з. намного отчетливее плоской вершины пучности напряжения для измерения зондом с детектором и вольтметром.