Приборы М-типа: ЛБВ-М и магнетрон. Движение заряженных частиц в скрещенном электрическом и магнитном полях

критическом режиме  при , - электрон пролетает по касательной к аноду,  и энергия электрона, сообщенная ему полным потенциалом анода, равна кинетической энергии, связанной только с азимутальной скоростью :

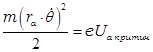. Отсюда получаем, с использованием найденного интеграла, соотношение между критическим анодным напряжением и индукцией магнитного поля  в критическом режиме:, и, далее, подставив , получаем  уравнение параболы критического режима.

Таким образом, длительное движение электронов вблизи анодных резонаторов возможно только при магнитном поле больше критического. Это необходимое условие работы магнетрона, но кроме него нужна еще синхронизация движения электрона с волной, бегущей по окружности анода.

Оценим теперь условия синхронизации. Определим среднюю фазовую скорость волны, бегущей по среднему радиусу окружности в пространстве между катодом и анодом, предполагая, что в соседних резонаторах поле колеблется в противофазе (так называемый p-вид колебаний). Обозначим среднюю длину периода N-резонаторной системы на этой окружности p, период колебаний T: , .

Средняя фазовая скорость  должна быть равна  средней скорости дрейфа электронов по этой окружности , т.к. для плоского случая (апроксимация спадающего по радиусу поля постоянным, т.е. как в плоской задаче ЛБВ-М). Приравняв эти две скорости получаем уравнение линии порогового потенциала (линии Хартри) , из которого находим . Одновременное выполнение условия синхронизации и условия закритичности режима дает ограничение зоны генерации магнетрона. Чтобы заторможенные электроны попадали на анод, нужно, чтобы анодное напряжение было больше потенциала синхронизации. В рабочей области возможно самовозбуждение магнетрона.

Оценим теперь КПД магнетрона. Скорость, которую электрон при ударе об анод зависит от того, на каком участке циклоиды он попал на анод. Наиболее вероятно и наименее благоприятно попадание на верхней части циклоиды . Таким образом .

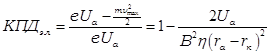Подставив сюда условие синхронизации (т.е. условие работы на определенной частоте колебаний)  получаем . Таким образом, КПД растет с ростом магнитного поля, количества резонаторов и длины волны.

 Резонансная система магнетрона

Анодный блок магнетрона – цепочка из N объемных резонаторов (N - четное). Резонаторы магнетрона связаны между собой в кольцо и являются замедляющей системой. Вообще в системе N связанных осцилляторов существует N типов колебаний. В замкнутой на себя кольцевой цепочке резонаторов возможны только колебания, для которых сумма  разности фаз  при обходе по окружности кратна :

(не дает азимутальных составляющих E и является стоячей ТЕМ волной вдоль оси магнетрона). Все виды колебаний, кроме  - т.н. p - вида колебаний, вырождены. Основной в магнетроне -  p - вид.  При работе на p - виде  колебаний в магнетроне устанавливается стоячая волна. Она состоит из двух из двух бегущих в противоположных направлениях. С одной из них и взаимодействует электронный поток.

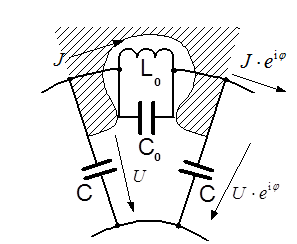
Оценим резонансные частоты замкнутой в кольцо цепочки резонаторов. Для этого воспользуемся эквивалентной схемой элемента периодичности, как изображено на рисунке. Для напряжений и токов в узлах можно написать уравнения , где – импеданс резонатора, и , где – импеданс емкости от анода к катоду. В результате получаем систему из двух однородных уравнений

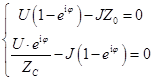, имеющую решение при равенстве нулю детерминанта

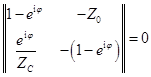
- это характеристическое уравнение для собственных частот. Обозначим  и, учитывая , получим спектр частот для разных видов колебаний:

.

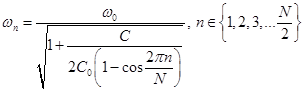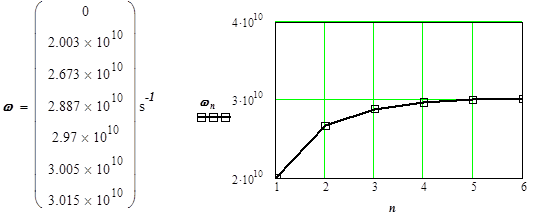
Для примера построим график со следующими величинами. Из графика можно видеть, что разделение (разность) частот возле p–вида наименьшая, поэтому есть опасность перескоков генерации с одного вида на другой при изменении режима магнетрона. Для увеличения разделения частот существуют разные конструктивные приемы. Часто применяются связки между резонаторами, вносящие индуктивность