Матпро включает: ленейное пргр-е, динамическое прогр-е, целочисленное прогр-е, дробнолинейное прогр-е и т.д. В 1939г. Л.В.Конторович выпустил брошюру матем. м-ды анализа и планир-я произв-ва. В Америки Дж. Данциг и Т. Кумпанс работали над теорией оптимихации. В 1951г. в их работе появляется термин «линейного програмир-е». В 1975г. Кумпанс и Конторович получили нобелевскую премию.Постановкой общей задачи МП: определить значение неизв-ых х1,х2,…хn, при которых выпол-ся ограничения gi(x1,x2,….xn) (<=,=, >=) bi(i=1,m)(1) и доставляется экстремум функции Z=f(x1,x2,…xn) –extr-(2) целевая функция или функция цели. Значение переменных (х1,х2,…хn) наз-ся решением задачи или планом. План удовлетворяющий ограничениям (1) наз-ся допустимым. Допустимый план, при котором значения достигают экстремума наз-ся оптимальным. Задачи МП : определение оптимального плана, опред-е оптимального объема выпуска продукции, опред-е оптим-го сочитания посевов с/хоз-ых культур, формир-е оптим-го пакета активов, максимиз-щий прибыль банка и т.д.
2. Экономические
примеры задач, решаемых методами МП. 1.Фирма изгот-т прод-цию,кот.хранится
на 2-х складах(A1 и А2) в кол-вах 170 и 190 тыс.ед. соотв-но.
Потребители прод-ции В1,В2 и В3 нужд-ся в след. кол-ве: 90,110,60. Стоимость
трансп-ки ед.прод-ции от поставщика Ai (![]() ) портебителю Bj (
) портебителю Bj (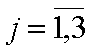 ) записано в
матрице:
) записано в
матрице: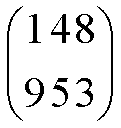 Затраты на
транспортировку м.б. описаны функцией
Затраты на
транспортировку м.б. описаны функцией
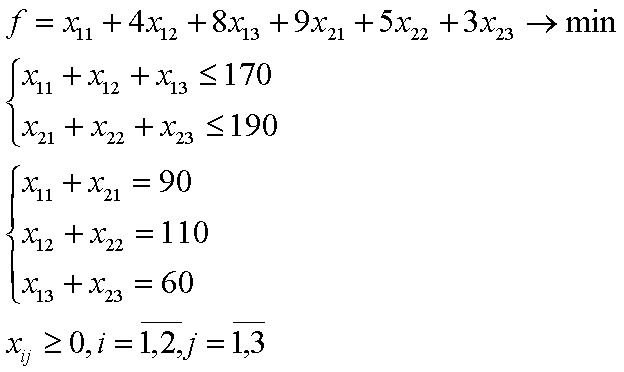
2.Предприятие может производить 2 вида продукции(П1,П2), используя для этого 3вида ресурсов сырье, оборудование и труд.
|
ресурс |
Расход ресурсов на ед.прод. |
Кол-во ресурсов |
|
|
П1 |
П2 |
||
|
Сырье,кг |
1 |
3 |
210 |
|
Фонд времени работы оборудования ст/час |
3 |
2 |
210 |
|
Труд, чел/час |
3 |
1 |
180 |
|
Прибыль от реализации ед.прод. |
35 |
49 |
|
Определить оптим. план выпуска продукции. Обозначим х1,х2 количество продукции П1 и П2 в оптимальном плане. Прибыль опишется функцией:
f= 35x1+49x2 – max
x1+3x2=210}
3x1+2x2<=210}
3x1+x2<=180 }
x1>=0,x2>=0
3. Необх.найти исполнителей 3-х работ.Для вып-я имеется 3
кандидатуры.Их пр-ть можно записать в виде матрицы: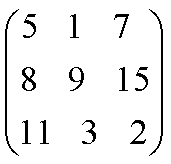 Найти опт.распр-е
исполн-ей при усл-и,что каждый исполн-ль вып-т только одну работу и на каждую
работу назн-ся 1 прибыль.
Найти опт.распр-е
исполн-ей при усл-и,что каждый исполн-ль вып-т только одну работу и на каждую
работу назн-ся 1 прибыль.
Обозн. хij-факт назнач-я или неназнач-я на i-тую работу
j-того исполнителя. 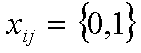 -булева переменная.
-булева переменная.
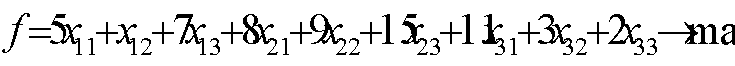
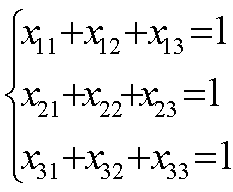
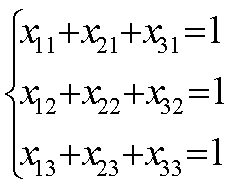
3. Различные формы записи ЗЛП (общая, каноническая, симметрическая)
Общей ЗЛП называют задачу максимизации (минимизации) линейной функции 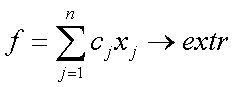 (1)
(1) 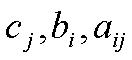 -некоторые
постоянные числа.
-некоторые
постоянные числа. 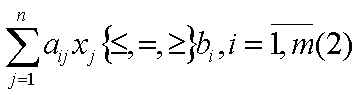
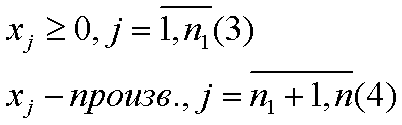
Симметрическойой формой записи ЗЛП наз-ся задача максимизации функции (1) при линейных ограничениях в неравенствах со знаком <=и не отрицательных переменных и задача минимизации функции (1) при линейных ограничениях в неравенствах со знаком >=и неотрицательных переменных. Канонической формой записи ЗЛП наз-ся задача максимальной функции (1) при линейных ограничениях равенствах и неотрицательных переменных. Любая другая форма называется смешанной.
min f(x) = -max(-f(x))
Преобразование нерав-ва в уравнение и наоборот осущ-ся на основе Леммы:
всякому решению х1…хn нерав-ва a1x1+…+anxn<=b (5)соответствует вполне определенное решение
х1…хn, xn+1 уравнения a1x1+…+anxn+xn+1=b (6)
при условии что хn+1>=0(7) и наоборот. Всякому решению x1…xn,xn+1
уравнения 6 и неравенства 7 соответствует решение x1…xn
неравенства (5). Если в зад-че есть опред.перем-я 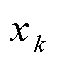 -произв. ,то ее
можно заменить разностью 2-х неотриц.пер-х (
-произв. ,то ее
можно заменить разностью 2-х неотриц.пер-х (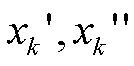 ) :
) :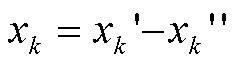
4. Геометрическая интерпретация целевой функции и ограничения ЗЛП. Геометрическая формулировка ЗЛП.
Пусть дана задача f=c1x1+c2x2-max (1)
a11x1+a12x2<=b1 }
am1x1+am2x2<=bm} (2)
x1>=0, x2>=0 (3)
План задачи (х1,х2) – точка на плоскости. Каждое неравенство с-мы (2) предст. собой полуплоскость. Полуплоскость –выпуклое множество. Выпуклым наз-ся множество в которым точки отрезка соединяющие (х1 и х2) принадлежащие этому множеству то же принадлежат множеству. С-ма (2) представляет собой пересечение полуплоскастей. При пересечении могут получиться:
1)выпуклая многоугольная замкнутая область.
2) выпуклая открытая многоугольная область
3) единственная точка
4) пустое множество
5) луч и отрезок
Геометрическая интерпретация целевой функции:функция (1) представляет
собой семейство параллельных прямых, которые наз-ют линиями уровня(линиями
постоянного значения целевой функции). Частные производные функции по х1 и х2
показывают скорость возрастания целевой функции вдоль координат осей.
Вектор-градиент показывает направление найскорейшего возрастания целевой
функции.Для задачи 1-3 вектор-градиент = 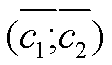 Выходит из точки
(0,0) и направлен в точку с координатами
Выходит из точки
(0,0) и направлен в точку с координатами![]() . Вектор-градиент
перпендикулярен линиям уровня. Пересечение полуплоскастей принято наз-ть
областью допустимых значений(ОДЗ).
. Вектор-градиент
перпендикулярен линиям уровня. Пересечение полуплоскастей принято наз-ть
областью допустимых значений(ОДЗ).
5. Графический метод решения ЗЛП.
Графический способ целесообразно использовать для решения задач с двумя переменными, записанных в симметричной форме, а также для задач со многими переменными при условии, что в их канонической записи содержится на более двух свободных переменных. Порядок решения ЗЛП графическим способом:
1. Построить ОДЗ; 2. Построить вектор 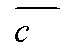 или
или ![]() 3. Перпендикулярно
3. Перпендикулярно![]() построить линию
уровня f=0. 4. Перемещая линию уровня в градиентном
направлении найти точку максимума или минимума ОДЗ; 5. Найти координаты точки
максимума (минимума) и значение функции в этой точке. В ходе решения ЗЛП граф.
способом могут получаться след. результаты:
построить линию
уровня f=0. 4. Перемещая линию уровня в градиентном
направлении найти точку максимума или минимума ОДЗ; 5. Найти координаты точки
максимума (минимума) и значение функции в этой точке. В ходе решения ЗЛП граф.
способом могут получаться след. результаты:
1. Оптимальный план единственный: линия уровня и ОДЗ в крайнем положении имеют одну общую точку;
2. Оптимальных планов бесконечное множество: в разрешающем положении линия уровня проходит через грань ОДЗ;
3. Задача не имеет решения: ОДЗ=ø;
4. Целевая функция не ограничена, в этом случаи добавляется еще одно ограничение.
Граф.способом можно решать задачи с большим чем 2 количественных переменных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.