Основы физической химии. Взаимодействие системы с окружающей средой. Максимальная работа расширения идеального газа. Термодинамический потенциал, страница 6

m_i = m⁰_i + RT lnP          ( 7 )

p_i – парциальное давление компонента i в смеси; m⁰_i – значение m_i при p_i = 1 бар. Химический потенциал характеризует способность данного компонента к выходу из данной фазы. Переход компонента может происходить самопроизвольно только из фазы, для которой его химический потенциал больше, в фазу, для которой он меньше, он выравнивается и достигается равновесие.

Химическое равновесие.

n₁А₁  + n₂А₂  =  n₃А₃  +  n₄А₄

При  T = const   и  Р = const   dG = Sm_idn_i  для конкретной реакции количество вещества n_i равно стехиометрическим коэффициента , находящимся в уравнении реакции.

DG = Sn_im_i подставим значение химического потенциала из уравнения (7) в данное выражение и сделаем соответствующие преобразования:

DG= S _in (m_i⁰ +RT ln p_i) = S (n_i m_i⁰ + RT n _i ln p_i) =   n_i m_i⁰ + S RTn_i ln p_i =

=  Sn_im_i⁰ + RT S ln = + RT D ln ( )

В случае химического равновесия DG = 0 и предыдущее равенство принимает вид:

D (n_im_i⁰) = - RT D ln ( )  раскроем значение скобок - это разница между логарифмами давлений продуктов и реагентов реакции. Получаем следующее выражение:

D (n_im_i⁰) = - RT ( ) = -RT ln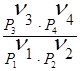

При постоянных температуре и давлении D (n_im_i⁰)  = const, значит 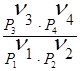  = const = K_P -  константа равновесия

D (n_im_i⁰)  = -RT ln K_P  из этого следует что:

DG = -RT ln K_P + RT ln 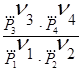 (8)   данное уравнение называется уравнение изотермы химической реакции и применяется для расчетов изменения энергии Гиббса в газообразной среде. Для растворов используют энергию Гельмгольца. При постоянных объеме и температуре энергия Гельмгольца имеет следующее значение:

DA = -RT ln K_C + RT ln 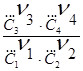   ;  С₁ , С₂ , С₃ , С₄  - концентрации

Если исходные парциальные давления веществ в уравнении (8) равны по 1, то уравнение (8) примет вид:

DG⁰ = - RTln K_P        (9)         уравнение нормального сродства

Зависимость константы равновесия от температуры.

Термодинамическая константа не зависит от парциальных давлений газов, а зависит от температуры. Приведем объединенное уравнение Гиббса-Гельмгольца.

Произведем в этом уравнении некоторые замены:

DG = Ty   ;     

Вместо y подставим значение энергии Гиббса  из уравнения нормального сродства:

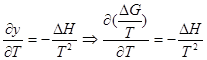;   Вынесем – R за значение дифференциала и поделим левую и правую части уравнения на – R

  Уравнение изобары химической реакции.

Аналогичное уравнение можно получить при постоянных объеме и температуре, но в этом случае используется энергия Гельмгольца, и константа включает в себя концентрации.

  Уравнение изохоры химической реакции.

ЧАСТЬ  2.    ОСНОВЫ КОЛЛОИДНОЙ  ХИМИИ.

Коллоидные системы это такие системы, в которые входят частицы крупнее, чем молекула, но мельче чем макротело. Коллоидная химия оперирует понятиями, сплошная фаза и дисперсная фаза.

Сплошная фаза- это фаза, которая не прерывается на всем своем протяжении.

Дисперсная фаза- это фаза, которая ограничена в пространстве сплошной фазой.

Коллоидная система обязательно является сильно раздробленной (мелко дисперсной). Дисперсность – величина обратная размеру частиц:

D = 1/r , измеряется в м^-1  или см^-1.

Классификация коллоидных систем по Оствальду.

Эта классификация основана на агрегатном состоянии фаз.

Обозначение	Название	Примеры
Т/Ж	Золи	Речная и сточная вода
Ж/Ж	Эмульсии	Молоко, крема, битум
Г/Ж	Газовые эмульсии	Лимонад, коктейль
Ж/Т	Гели	Кисель, холодец
Г/Т	Ксерогели	Канифоль, мел, пемза
Т/Т	Тверд. колл. Растворы	Сталь, малахит, яшма
Т/Г		Дым, пыль
Ж/Г	Аэрозоли	Туман, тучи
Г/Г		Атмосфера Земли