Плоскость. Различные способы задания плоскости на чертеже. Следы плоскости

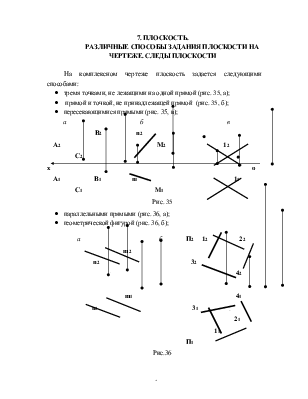
следами плоскости (частный случай задания плоскости двумя пересекающимися прямыми, рис. 37).

Каждый из перечисленных способов задания плоскости допускает переход к любому другому.

Положение плоскости относительно плоскостей проекций удобно определять по ее следам. Линия пересечения плоскости с плоскостью проекций называется следом плоскости(рис. 37, а, б).

аб

                                            z

         П2                             Qz                                                            Qz

                           Q2                                                         Q2                  Q3

                                                                 П3           Qх                            Qу

                                       Q          Q3

x      Qx                                       о                                 Q1               Qу

Q1                       Qу

                        П1                                             y

                                                       Рис. 37

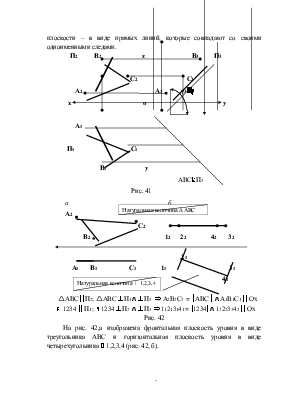
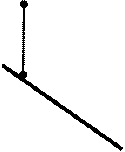
На рис. 37,а,б изображена плоскость Q, занимающая в пространстве общее положение. Различают три следа плоскости Q1 – горизонтальный(на горизонтальной плоскости проекций), Q2 – фронтальный(на фронтальной плоскости проекций), Q3 – профильный(на профильной плоскости проекций).

Любые два следа плоскости, как две пересекающиеся прямые, вполне определяют положение плоскости в пространстве и на чертеже. Третий след плоскости всегда можно построить по двум данным.

Следует заметить, что следы плоскости общего положения Q попарно пересекаются на осях в точках Qx, Qy, Qz (рис.37). Эти точки называются точками схода следов.

Вопросы для самоконтроля

1.Сколько прямых линий можно провести в одной плоскости?

2.Каким образом задается плоскость на чертеже?

3.Что называется следом плоскости?

4.Сколько следов имеет плоскость общего положения и как они называются?

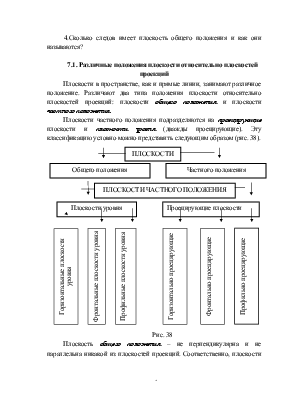
7.1. Различные положения плоскости относительно плоскостей проекций

Плоскости в пространстве, как и прямые линии, занимают различное положение. Различают два типа положения плоскости относительно плоскостей проекций: плоскости общего положения и плоскости частного положения.

Плоскости частного положения подразделяются на проецирующие плоскости и плоскости уровня (дважды проецирующие). Эту классификацию условно можно представить следующим образом (рис. 38).

Рис. 38

Плоскость общего положения – не перпендикулярна и не параллельна никакой из плоскостей проекций. Соответственно, плоскости частного положения либо параллельны, либо перпендикулярны плоскостям проекций. 

Плоскости уровня и проецирующие плоскости относятся к плоскостям частного положения.

 Проецирующие плоскости – перпендикулярны одной из плоскостей проекций. В зависимости от этого их подразделяют на три вида: горизонтально проецирующие (рис.39,а,б), фронтально проецирующие(рис. 40,а, б) и профильно проецирующие (рис. 41).

На рис. 39,а,б изображена горизонтально проецирующая плоскость Q, заданная треугольником АВС. Горизонтальная проекция такой плоскости (А1В1С1) представляет собой прямую, которая одновременно является горизонтальным следом плоскостиQ1.

Фронтальная проекция плоскости Qопределяется проекциейтреугольника А2В2С2 на эпюре, а фронтальный след плоскости Q2расположен перепендикулярно оси Х. Угол α, который образуется между плоскостью треугольника АВС и  П2, проецируется на плоскость П1 без искажения и определяет угол наклона плоскости к фронтальной плоскости проекций (рис.39,б).

а                                                      б

                                                           Q2                                   А2

П2

               А                                                        В2

              В                         Q                                                            С2

      ∙                                                   Qх  ∙                                         

       В1   А1              С                                                     a1a

С1                                            В1

П1                                                           А 1

С1

                                                     АВСП1                                                               Q1

Рис. 39

На рисунке 40,а изображен эпюр фронтально проецирующей плоскости Q, заданной треугольником MNK, который проецируется на фронтальную плоскость проекций в виде прямой линии (M2K2N2) и совпадает с фронтальным следом плоскости Q2. Горизонтальный след плоскости Q1перпендикулярен оси Х.

Угол β между плоскостью треугольника и П1 проецируется на П2 без искажения и является углом наклона плоскости МNK  к горизонтальной плоскости проекций (рис.40,а).

а                                                        б

M2Q2

П2                   М2

N2                                                              N2

K2                                                                              N                            М

β 2ºbП2K2

Qx                                            П1                                                                      Q

N1                                                                       K

П1

M1

Q1      K1MKNП2

Рис. 40

Профильно проецирующая плоскость перпендикулярна профильной плоскости проекций (рис.41). Профильные проекции всех точек этой плоскости совмещаются с профильным следом (А3С3В3). Угол наклона γ определяет угол наклона плоскости треугольника