Определение натуральной величины фигуры сечения. Построение разверток поверхностей геометрических тел

а                                 б                            в

Рис. 71

           а                                 б                            в

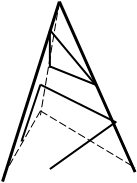Рис. 72

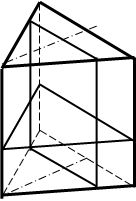
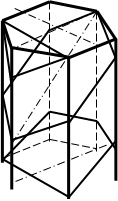
На фронтальной проекции фигура сечения пирамиды совпадает с проекцией плоскости и изображается отрезком. Горизонтальная и профильная проекции фигуры сечения строятся в проекционной связи. Искомые точки лежат на  пересечении  линий связи с ребрами пирамиды (рис.72).

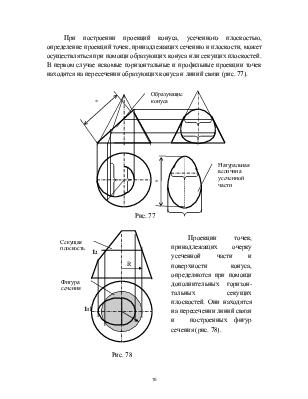
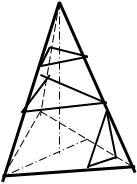
При построении проекций усеченных плоскостью многогранников определяют проекции фигуры сечения, вершины которой находятся на ребрах  (точки пересечения ребер многогранника с секущей плоскостью). Вначале находят точки, принадлежащие фигуре сечения, на  фронтальной проекции. На других проекциях изображение усеченной части выявляется  с помощью линий связи (рис 73.).

На фронтальной проекции фигура сечения пирамиды совпадает с проекцией плоскости и изображается отрезком. Горизонтальная и профильная проекции фигуры сечения строятся в проекционной связи. Искомые точки лежат на  пересечении  линий связи с ребрами пирамиды (рис. 73).

                                     12º32  3313

                                                 4 3

          22º 42                   23  1

                                                 3

                  41                31  4                        

                                                2

                  21                 11

Рис. 73

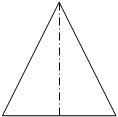
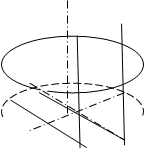
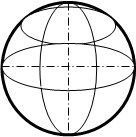
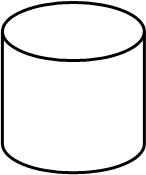
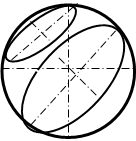
При пересечении различных  поверхностей вращения  плоскостью,  фигура сечения может представлять собой различные фигуры. Как правило, ими являются различные кривые линии. Фигурой сечения сферы всегда  является окружность, диаметр которой зависит от положения секущей плоскости относительно экватора (рис.74, а).

Фигуры сечения конуса  могут быть как кривые линии, так и прямые. Если секущая плоскость располагается перпендикулярно к оси конуса, то фигура сечения будет являться окружностью. Если секущая плоскость проходит через вершину, а также ось симметрии конуса, то фигура сечения отображается прямыми линиями или повторит очерк конуса (рис.74, б). Если секущая плоскость наклонена к оси вращения  и пересекает все образующие конуса, в сечении получается эллипс. Когда секущая плоскость параллельна одной из образующих конуса, в сечении получается парабола (рис. 75, б).   Если секущая плоскость параллельна оси вращения конуса или расположена так, что угол наклона между секущей плоскостью и  осью вращения будет меньше, чем угол между осью вращения и образующей,   то  сечением будет  гипербола (рис. 75, б).

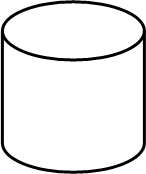
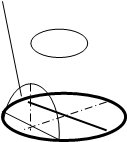
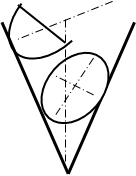
Фигурами сечения цилиндра являются окружность, если секущая плоскость параллельна основанию. Если секущая плоскость располагается параллельно оси вращения или совпадает с ней, то сечение изображается прямоугольником (рис.75, в).

              а                             б                                     в

                               Гипербола

Рис. 74

а                             б                                     в

                          Парабола

Рис. 75

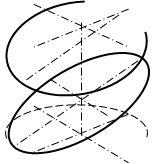
В частном случае, когда диаметр цилиндра равен его высоте и секущая плоскость проходит через ось вращения, фигура будет выглядеть    квадратом. При рассечении цилиндра наклонной плоскостью сечение представляет собой эллипс или его часть (рис.75, в).

9.1 Определение натуральной величины фигуры сечения

Изобразить натуральную величину фигуры сечения можно различными способами. Мы предлагаем  достаточно простое построение (см. рис. 76).

На свободном поле чертежа рядом от  заданной секущей плоскости, на фронтальной проекции, восстанавливаются перпендикуляры. Это  позволяет определить истинную величину высоты фигуры, так как при подобном расположении секущей плоскости данный размер спроецирован на фронтальной проекции в натуральную величину. Размеры ширины фигуры сечения переносятся с горизонтальной или профильной проекции. Именно на этих проекциях требуемые размеры отображены без искажения. Имеющиеся величины ширины фигуры сечения откладываются на проведенных перпендикулярах (рис.76). 

                                                *

                    3                       1

                     *   

                                                         1213

               4                        2               

ø

                                  22º32                       33                                      23                

                            42

                                                 31                       43                                                  1

                                                                                            3

                             41                          11

                    ø                                        *                                                  

                                                                                     4                      2  

                                            21

Рис. 76

Таблица 7

Алгоритм построения натуральной величины фигуры сечения