Исследование многосвязных систем автоматического регулирования (Лабораторная работа № 16)

Лабораторная работа  № 16 (LTAU16)

ИССЛЕДОВАНИЕ МНОГОСВЯЗНЫХ САР

Цель работы:

-  получить представление об основных понятиях, особенностях, принципах построения и функционирования многосвязных систем автоматического регулирования (САР);

-  путем имитационных экспериментов в среде СППП MVTU получить навыки исследования многосвязных САР.

Системы, в которых регулируются несколько величин, называют многомерными или многосвязными. Примерами многосвязных систем могут служить: паровой котел, в котором одновременно регулируются давление пара, его температура, разрежение в топке, процент CO₂; самолет, у которого регулируются курс, угол тангажа, угол крена, скорость, высота; прокатный стан, где регулируются скорость и толщина прокатываемой полосы и т. д.

В терминах “многомерные” и “многосвязные” системы понятия “мерности” и “связности” не совпадают с понятием порядка или размерности системы. Так, в двухмерной системе, в которой регулируются две величины, порядок уравнения, определяющий размерность системы, может быть любым.

Для многосвязных систем характерно наличие связей между регулируемыми величинами. Связи эти могут быть двух родов. Первый род связей обусловлен физическими свойствами регулируемого объекта. Так, если мы увеличиваем подачу топлива в котел, то при этом повышаются и температура и давление пара. Увеличение скорости вращения синхронной машины одновременно приводит к увеличению частоты и напряжения переменного тока. Связи первого рода будем называть внутренними связями. Второй род связей накладывается на систему по условиям, определяемым технологическим процессом. Например, летчику могут задаваться отдельно курс и высота полета, а скорость должна регулироваться таким образом, чтобы обеспечивался минимальный расход топлива. В этом случае требуется, чтобы часть регулируемых координат была независимой друг от друга (курс и высота), а координаты другой части (высота и скорость) были связаны между собою, причем эта связь определяется выбранным для системы критерием оптимальности. В системах контурного программного управления копировальным станком подачи по осям связываются через контур обрабатываемого изделия. Связи, обусловливающие требуемую зависимость (или независимость) регулируемых координат друг от друга, как правило, не существуют в объекте. Более того, существующие в нем внутренние связи обычно обеспечивают не ту зависимость, которая требуется. Устранение противоречия между существующей и требуемой зависимостями регулируемых координат друг от друга достигается введением дополнительных регулирующих органов и связей второго рода, которые мы будем называть внешними связями.

Как показано на рисунке 1, входы и и выходы у многомерных объектов влияют друг на друга, что приводит к взаимозависимости цепей прямой передачи сигналов u₁→y₁, u₂→y₂ и т.д. Внутренняя структура многомерных объектов оказывает существенное влияние на проектирование многомерных систем управления. Такая структура может быть получена в результате теоретического моделирования, если знания об объекте оказываются достаточными. Структуры различных технологических объектов имеют существенные отличия и поэтому не могут быть описаны небольшим набором стандартизованных структур. Однако реальные структуры часто можно привести к канонической форме, используя преобразования подобия или простые правила преобразования блок схем.

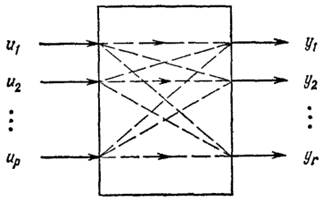
Рисунок 1. Многомерный объект

Канонические структуры. В качестве примера рассмотрим блок-схему испарителя и перегревателя парового котла с естественной циркуляцией, изображенную на рисунке 2. Регулируемыми переменными этого двумерного объекта являются давление пара y₂ в парособирателе и температура пара y₁ на выходе перегревателя.

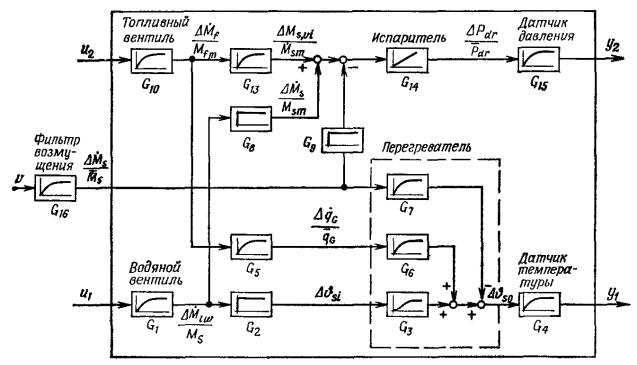
Рисунок 2. Блок-схема испарителя и перегревателя парового котла с естественной циркуляцией

Управляющими переменными являются расход топлива u₂ и расход воды u₁. На основании блок-схемы запишем следующие непрерывные передаточные функции:

Перегреватель:

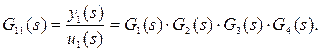
Испаритель:

·

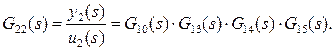Связь перегреватель—испаритель:

·

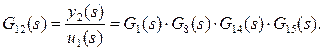Связь испаритель—перегреватель:

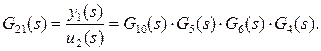
Элементы с передаточными функциями G₁₁ и G₂₂ называют главными, а элементы с передаточными функциями G₁₂ и G₂₁ — элементами связи. Предполагая, что входные и выходные сигналы квантуются синхронно с тактом квантования Т₀, получим, применяя z-преобразование, соответствующие дискретные передаточные функции указанных элементов относительно квантователей:

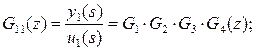
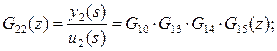
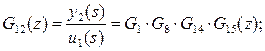                                                       (1)

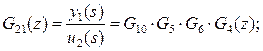
Из приведенного примера видно, что в этом представлении относительно