Интерполяционная формула Лагранжа. Интерполяционная формула Ньютона. Построение эмпирических формул методом наименьших квадратов. Нахождение собственных значений и собственных векторов матриц

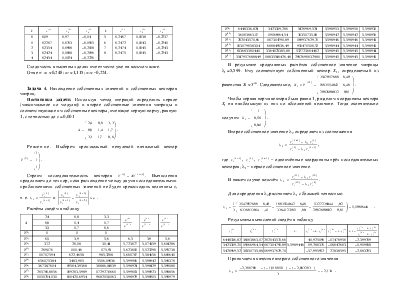
Вывести эмпирическую формулу зависимости нагрузки от времени. Характер зависимости установить графически. Определить погрешность вычислений.

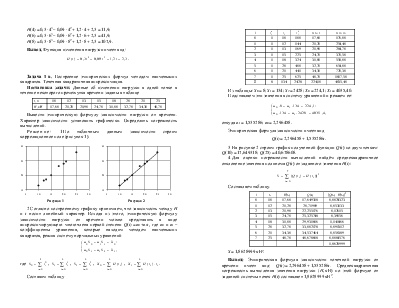
Решение: 1 По табличным данным зависимости строим корреляционное поле (рисунок 1).

Рисунок 1	Рисунок 2

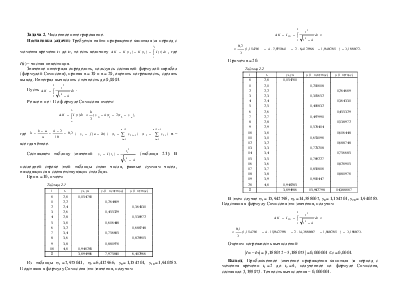
2 Согласно построенному графику принимаем, что зависимость между H и t носит линейный характер. Исходя из этого, эмпирическую формулу зависимости нагрузки от времени можно представить в виде аппроксимирующего многочлена первой степени Q(t) = a₀ +a₁t, где a₀ и a₁ – коэффициенты уравнения, которые находим методом наименьших квадратов, решив систему нормальных уравнений

где , , , , .

Составим таблицу

i
0	1	10	100	17,60	176,00
1	1	12	144	21,20	254,40
2	1	13	169	21,90	284,70
3	1	15	225	24,70	370,50
4	1	18	324	31,00	558,00
5	1	20	400	32,70	654,00
6	1	21	441	34,30	720,30
7	1	25	625	40,70	1017,50
S	8	134	2428	224,10	4035,40

Из таблицы: S₀ = 8; S₁ = 134; S₂ = 2428; X₀ = 224,1; X₁ = 4035,40.

Подставляем эти значения в систему уравнений и решаем ее:

откуда a₁ = 1,535286; a₀ = 2,296458.

Эмпирическая формула зависимости имеет вид

                                        Q(t) = 2,296458 + 1,535286t.

3 На рисунке 2 строим график полученной функции Q(t) по двум точкам: Q(10) = 17,649318; Q(25) = 40,678608.

4 Для оценки погрешности вычислений найдём среднеквадратичное отклонение значения полинома Q(t) от заданного значения Н(t):

 

Составляем таблицу.

S = 1,8628999 кН².

Вывод: Эмпирическая формула зависимости точечной нагрузки от времени имеет вид: Q(t) = 2,296458 + 1,535286t. Среднеквадратичная погрешность вычисления значения нагрузки (Н, кН) по этой формуле от заданной системы точек Н(t) составляет 1,8628999 кН².

Задача 2. Численное интегрирование.

Постановка задачи: Требуется найти приращение капитала за период с момента времени t₁ до t₂, то есть величину , где I(t) – чистая инвестиция.

Значение интеграла определить, пользуясь составной формулой парабол (формулой Симпсона), приняв n = 10 и n = 20, оценить погрешность, сделать вывод. Интеграл вычислить с точность до 0,0001.

Пусть .

Решение: По формуле Симпсона имеем:

где ; ; ; ; n – всегда чётное.

Составляем таблицу значений  (таблица 2.1). В последней строке этой таблицы стоят числа, равные суммам чисел, находящихся в соответствующих столбцах.

При n = 10, имеем

Таблица 2.1

Из таблицы s₁ = 7,975041, s₂ = 6,412966, y₀ = 1,154701, y₁₀ = 1,940285. Подставив в формулу Симпсона эти значения, получим

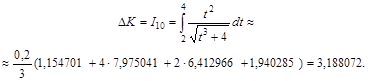
Примем n = 20.

Таблица 2.2

i	ti	y0, y20	yi (i – нечётное)	yi (i –чётное)
0	2,0	1,154701
1	2,1		1,211018
2	2,2			1,264609
3	2,3		1,315652
4	2,4			1,364331
5	2,5		1,410832
6	2,6			1,455329
7	2,7		1,497991
8	2,8			1,538972
9	2,9		1,578414
10	3,0			1,616448
11	3,1		1,653190
12	3,2			1,688748
13	3,3		1,723218
14	3,4			1,756685
15	3,5		1,789227
16	3,6			1,820915
17	3,7		1,851810
18	3,8			1,881970
19	3,9		1,911447
20	4,0	1,940285
S		3,094986	15,942798	14,388007

В этом случае s₁ = 15,942798, s₂ = 14,388007, y₀ = 1,154701, y₂₀ = 1,940285. Подставив в формулу Симпсона эти значения, получим

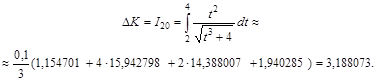
Оценим погрешность вычислений:

|I₁₀ – I₂₀| = |3,188072 – 3,188073| = 0,000001 £ e = 0,0001.

Вывод. Приближенное значение приращения капитала за период с момента времени t₁ = 2 до t₂ = 4, полученное по формуле Симпсона, составило 3,188073. Точность вычисления – 0,000001.

Задача 3 а. Численные методы решения систем линейных алгебраических уравнений (СЛАУ). Метод итераций.

Постановка задачи. Методом итераций решить систему линейных уравнений с точностью до 0,001, предварительно оценив число необходимых для этого шагов

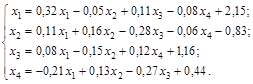
Решение. Число шагов, дающих наверняка ответ с точностью до 0,001, определим с помощью соотношения

.

Т.к. первая норма матрицы, составленной из коэффициентов при неизвестных в правых частях уравнений системы,  равна

то итерационный процесс сходится; . Имеем

; ;

;

; .

Вычисления располагаем в таблице:

Сходимость в тысячных долях имеет место уже на девятом шаге.

Ответ: x₁ » 3,571; x₂ » –0,957; x₃ » 1,489; x₄ » –0,836.

Задача 3 б. Численные методы решения систем линейных алгебраических уравнений (СЛАУ). Метод Зейделя.

Постановка задачи. Методом Зейделя решить с точностью до 0,001 систему линейных уравнений, приведя её к виду, удобному для итераций, и оценив число необходимых для этого шагов

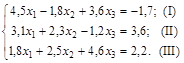
Решение. Приведём систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк:

 

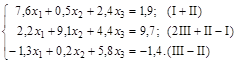
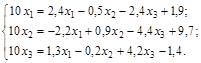
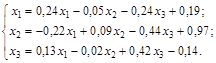
Число шагов, дающих наверняка ответ с точностью до 0,001, определим с помощью соотношения

.

Т.к. первая норма матрицы, составленной из коэффициентов при неизвестных в правых частях уравнений системы,  равна

то итерационный процесс сходится; . Имеем

; ;

;

; .

Вычисления располагаем в таблице:

Сходимость в тысячных долях имеет место уже на восьмом шаге.

Ответ: x₁ » 0,248; x₂ » 1,115; x₃ » –0,224.

Задача 4. Нахождение собственных значений и собственных векторов матриц.

Постановка задачи. Используя метод итераций определить первое (максимальное по модулю) и второе собственные значения матрицы и соответствующие им собственные векторы, имеющие первую норму, равную 1, с точностью до e = 0,001

.

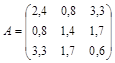Решение. Выберем произвольный ненулевой начальный вектор .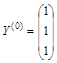

Строим последовательность векторов . Вычисления продолжаем до тех пор, пока расхождение между двумя последовательными приближениями собственных значений не будет превосходить величины e, т. е.  и .

Расчёты сведём в таблицу

A	2,4	0,8	3,3
	0,8	1,4	1,7
	3,3	1,7	0,6
Y(0)	1	1	1
Y(1)	6,5	3,9	5,6	6,5	3,9	5,6
Y(2)	37,2	20,18	31,44	5,723077	5,174359	5,614286
Y(3)	209,176	111,46	175,93	5,623011	5,523290	5,595738
Y(4)	1171,7594	622,4658	985,3208	5,601787	5,584656	5,600641
Y(5)	6561,75384	3483,905	5516,19036	5,599916	5,596942	5,598370
Y(6)	36738,7614	19504,39368	30886,14039	5,598924	5,598429	5,599180
Y(7)	205700,8056	109203,5989	172927,0661	5,599013	5,598923	5,598856
Y(8)	1151704,131	611421,6954	968215,0163	5,598929	5,598915	5,598979
Y(9)	6448336,824	3423319,206	5420969,524	5,598953	5,598950	5,598931
Y(10)	36103863,17	19166964,54	30351735,88	5,598942	5,598942	5,598950
Y(11)	202143571,66	107314791,89	169937629,71	5,598946	5,598946	5,598943
Y(12)	1131790583,54	600849536,49	951471510,52	5,598944	5,598944	5,598945
Y(13)	6336833014,41	3364123385,80	5327236044,02	5,598945	5,598945	5,598944
Y(14)	35479576888,49	18835540426,48	29826900329,81	5,598945	5,598945	5,598945

В результате проделанных расчётов собственное значение матрицы