Исходные данные
Момент инерции сечения 
м4
Модуль Юнга 
Па
Длина стержня 
м
Функция изменения осевого момента инерции поперечного
сечения: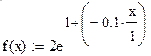 
Решение
Найдем критическую силу для разбиения стержня на: 
участков
Шаг разбиения стержня: 
Коэффициенты при неизвестных в системе линейных уравнений представленных далее в матричном виде:
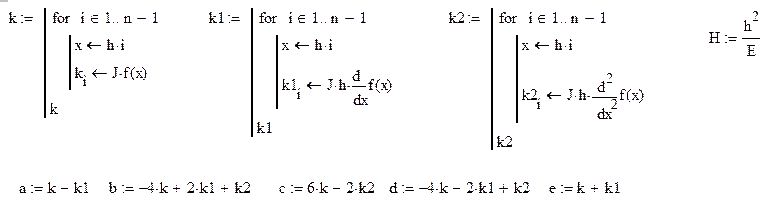
Найдем критическую силу:
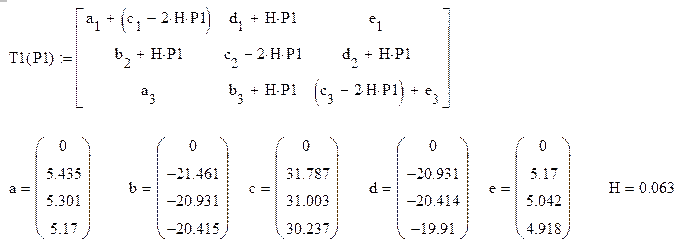
Определитель матрицы Т1 (уравнение критической силы для заданного стержня)
Коэффициенты при кубическом полиноме (определителе матрицы Т1)
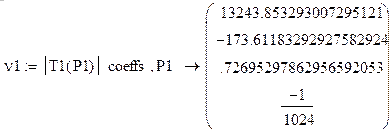
Решение кубического уравнения производим с помощью встроенной функции – polyroots
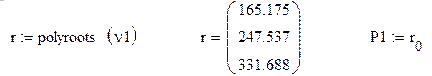
Критическая сила при данном числе разбиения стержня: 
EJ/l2
Находим прогибы стержня при данных условиях:
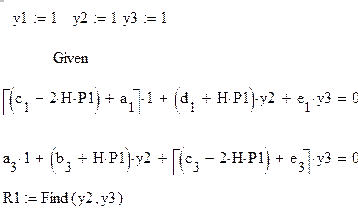
Формируем функцию прогиба оси стержня:
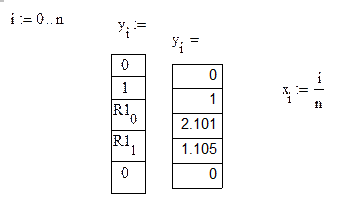
Найдем критическую силу для разбиения стержня на: 
участков
Шаг разбиения стержня:
Коэффициенты при неизвестных в системе линейных уравнений представленных далее в матричном виде:
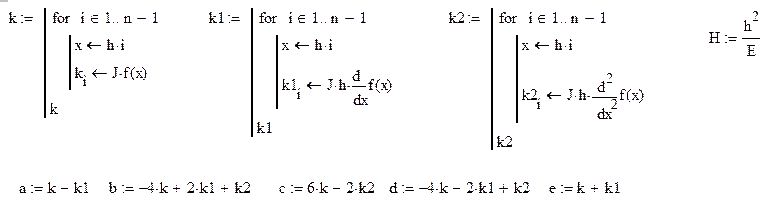
Найдем критическую силу:
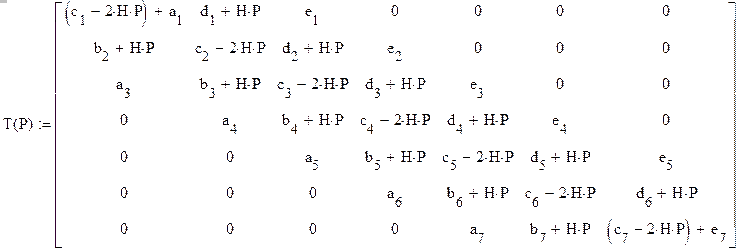
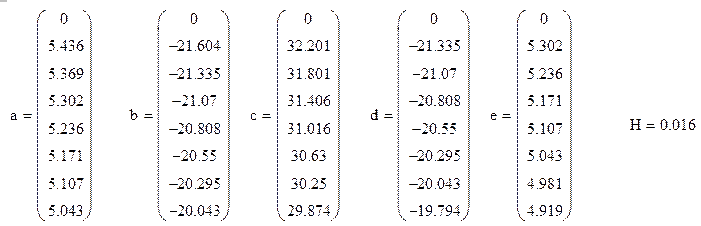
Определитель матрицы Т (уравнение критической силы для заданного стержня)
Коэффициенты при полиноме седьмой степени (определителе матрицы Т)
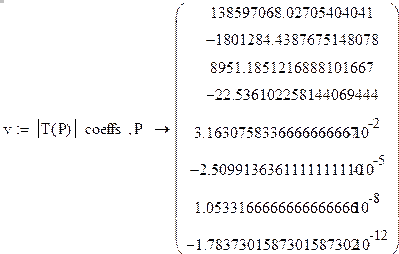
Решение уравнения седьмой степени производим с помощью встроенной функции – polyroots
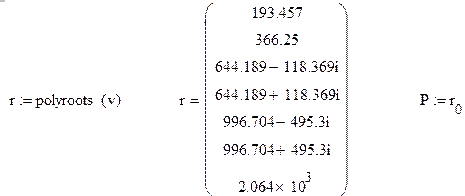
Критическая сила при данном числе разбиения стержня: 
EJ/l2
Находим прогибы стержня при данных условиях:
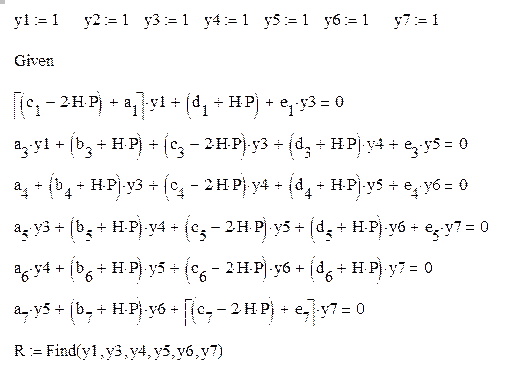
Формируем функцию прогиба оси стержня:
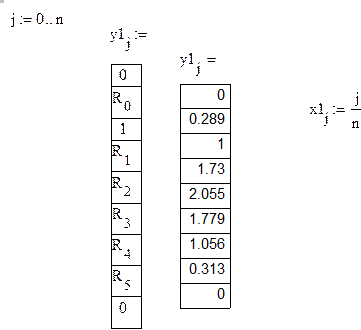
Конфигурация продольного сечения стержня в соответствии с законом изменения J(x)
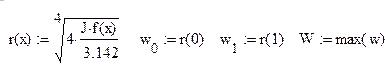
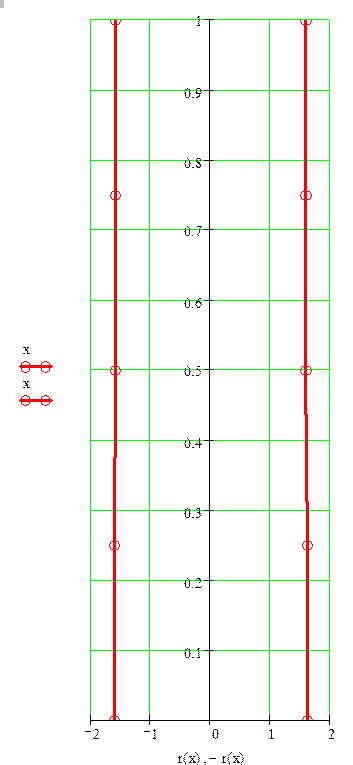
Форма потери устойчивости стержня
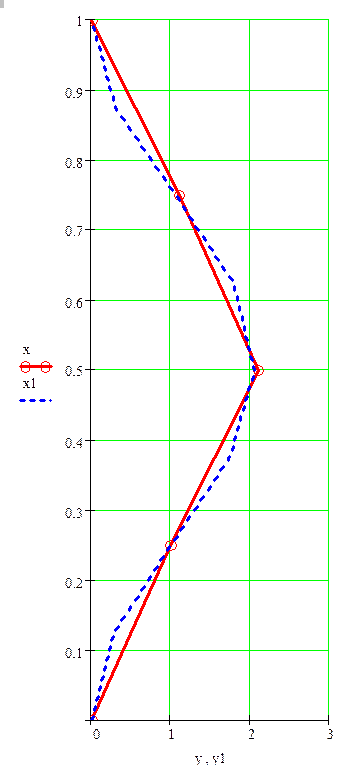
у – прогиб стержня при первом приближении (n=4)
у1 – прогиб стержня при втором приближении (n=8)
Сравнение в процентном отношении отличие Р1 от Р:
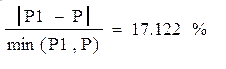
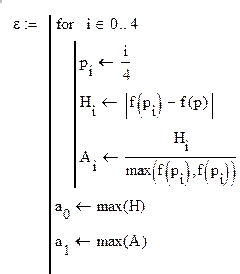
Используя кубическую норму, мы
оценили разности векторов прогибов первого и второго приближений в
совпадающих узлах: 
Отличие перемещений при n=4 и n=8 в процентном выражении: 
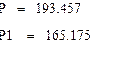
Минимальная критическая сила 
Fmin=165.175
EJ/l2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
