Лабораторная работа № 3
1. Цель работы: изучение теории симметричных составляющих и применение ее к анализу двухфазного КЗ.
Расчеты КЗ трехфазных симметричных схем производятся на одну фазу вследствие подобия явлений, происходящих в каждой из фаз и равенства по фазам значений одноименных величин.
При несимметрии в произвольной точке сопротивления в фазах неодинаковы и по этим причинам явления по фазам различны. Неодинаковы в этом случае величины токов, напряжений и углы сдвига между ними в различных фазах. Для определения токов и напряжений в любой фазе несимметричной системы необходимо составить трехфазную схему замещения и написать необходимое число уравнений, что усложняет решение задачи.
Сравнительно просто расчеты несимметричных режимов в трехфазных симметричных сетях осуществляются с помощью метода симметричных составляющих. Вычисление токов и напряжений с помощью метода симметричных составляющих сводится к вычислению этих величин при некотором фиктивном трехфазном КЗ, что представляет возможность вновь воспользоваться однолинейной схемой замещения и вести расчет на одну фазу. В этом состоит одно из основных достоинств метода симметричных составляющих.
Произвольную несимметричную систему трех векторов (токов, напряжений или потоков) A; B; C можно разложить однозначно на три симметричные системы:
– систему векторов прямой последовательности A1; B1; C1;
– систему векторов обратной последовательности A2; B2; C2;
– систему векторов нулевой последовательности A0; B0; C0.
Согласно условию разложения имеем:
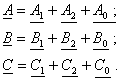 (3.1)
(3.1)
Введение оператора фазы а позволяет любой вектор каждой симметричной трехфазной системы выразить через один вектор той же системы.
Если принять в качестве основной фазу А, то систему (3.1) при помощи оператора а можно представить в следующем виде:
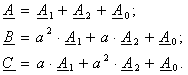 (3.2)
(3.2)
Совместное решение уравнений (3.2) дает:
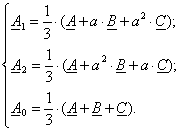 (3.3)
(3.3)
На рис. 3.1 показан пример разложения несимметричной системы на симметричные составляющие.
Системы прямой и обратной последовательности являются симметричными и уравновешенными, а система нулевой последовательности является симметричной, но неуравновешенной. Система нулевой последовательности может существовать только в неуравновешенных системах, которые характеризуются следующими условиями:
А + В + С ![]() 0. (3.4)
0. (3.4)
Геометрическая сумма неуравновешенной системы фазных токов равна утроенному току нулевой последовательности, который протекает в земле или в нулевом проводе.
На основании принципа независимости действия симметричных составляющих, который состоит в том, что в симметричной трехфазной системе напряжение любой последовательности может вызвать только токи одноименной последовательности.
В соответствии с вышеизложенным, для произвольного несимметричного КЗ основные уравнения второго закона Кирхгофа отдельно для каждой последовательности будут иметь вид:
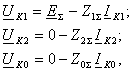 (3.5)
(3.5)
где Uк1, Uк2,.Uк0, Iк1, Iк2, Iк0 – симметричные составляющие напряжений и токов; ЕΣ – результирующая ЭДС; Z1Σ, Z2Σ, Z0Σ – результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.
Уравнения (3.5) содержат шесть неизвестных величин: три составляющих напряжения и три составляющих тока. Недостающие уравнения для определения этих величин получают из граничных условий, которыми характеризуются тот или иной вид несимметричного КЗ.
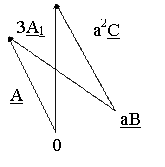
Исходная система

Прямая последовательность 3А1 = А + аВ + а2С.
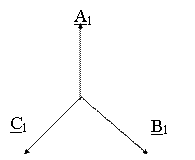
Обратная последовательность 3А2 = А + а2В + аС.


Нулевая последовательность 3А0 = А + В + С.
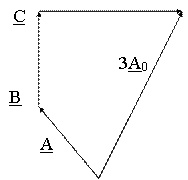

Проверка: А = А1 + А2 + А0.
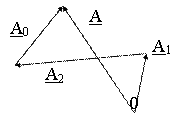
Рис. 3.1. Разложение несимметричной системы трех векторов на симметричные составляющие
При КЗ фаз В и С граничные условия будут для точки К (рис. 3.2,а):
![]() ; (3.6)
; (3.6)
![]() (3.7)
(3.7)
![]() . (3.8)
. (3.8)
Поскольку ток через землю отсутствует, то ![]() Следовательно (3.6) можно
переписать
Следовательно (3.6) можно
переписать
![]() .
.
Откуда
![]() . (3.9)
. (3.9)
Токи поврежденных фаз в месте КЗ выразим через ток прямой последовательности:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.