Импульсно-кодовая и дельта-модуляции

2.4. Импульсно-кодовая и дельта-модуляции

При импульсно-кодовой модуляции (ИКМ), как и при других способах, предназначенных для временного разделения каналов, цепь предоставляется последовательно различным передачам на короткие отрезки времени. Однако каждое данное значение кривой сигнала передается не изменением продолжительности, местоположения или амплитуды импульса, а соответствующей комбинацией более кратковременных импульсов - так называемым кодом.

Если код будет состоять из ограниченного числа импульсов, то и количество возможных комбинаций, которые могут быть использованы для передачи соответствующих мгновенных значений, будет ограничено.

Действительно, если для целей ко­дирования взять всего два импульса, то из них можно составить, исклю­чая нулевую, только три комбина­ции (1; 2 и 1 + 2). Из трех импульсов можно составить семь комбинаций (1;2; 1+2; 3; 1 + 3; 2 + 3 и 1+2 + 3); из пяти-31 комбинацию; из семи-127 комбинаций; из п импульсов-(2"-1) комбинаций.

На рис. 2.10, а изображена кривая сигнала (сплошная линия), который должен быть передан в моменты, отмеченные на оси времени. По оси ординат отложены как мгновенные значения сигнала, так и разрешен­ные для передачи фиксированные значения (напряжения или тока), ко­торые соответствуют комбинациям, изображенным на правой вертикаль­ной оси.

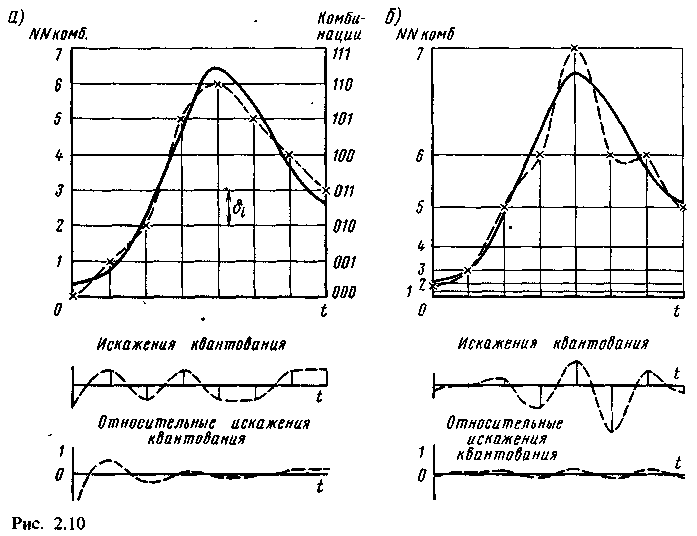
Передача ближайшего разрешен­ного значения вместо требуемого мгновенного значения сигнала назы­вается квантованием сигнала. Возни­кающие при этом искажения на­зываются 'искажениями квантова­ния.

Эти искажения, вводимые на пере­дающей станции, не могут быть уничтожены ни в линейном тракте, ни на приемной станции. Величина этих искажений изображена в ниж­ней части рис. 2.10, а.

Оценить искажения квантования можно (считая, что мгновенные значения напряжения сигнала являются случайной величиной), используя понятие дисперсии [см. выражение (1.1)].

Для i-го шага квантования (), соответствующего  -разрешенно­му значению напряжения, можно написать

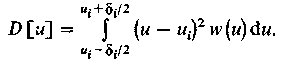
Принимая шаг квантования , ма­лым, можно приближенно считать, что плотность вероятности появле­ния мгновенного значения сигнала внутри данного шага квантования есть величина постоянная и равная.

Тогда получим

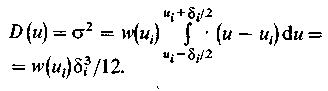
Определяя вероятность попадания данного мгновенного значения на­пряжения в i-и интервал квантова­ния

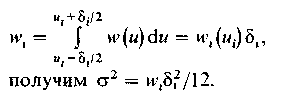
Общая суммарная дисперсия иска­жений квантования от всех шагов квантования . Но будет равна единице, так как можно считать, что каждое данное значение сигнала обязательно попадает в один из шагов квантования.

Тогда получим, что общая сум­марная дисперсия (мощность) иска­жений при равномерном квантова­нии ( - постоянная величина) .

Искажения квантования оценива­ются по логарифмическому отноше­нию мощности сигнала и мощности искажений квантования а_кв=lO*lg* *Р_с//12. Подставляя значения мощности сигнала Р_с = (и   =, где  - амплитуда сиг­нала; -порог ограничения и n-число разрядов кода, получим

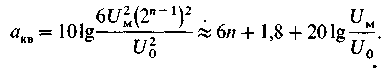
Следовательно, с увеличением п на каждую единицу акв возрастает на 6 дБ [12].

Возвращаясь к рис. 2.10, а, заме-1 им, что независимо от мгновенного значения сигнала искажения кванто­вания определяются шагом кван­тования /2. В то же время мешаю­щее действие любой помехи или ис­кажения определяет их относитель­ное значение. Если учесть, что при равномерном квантовании искаже­ния квантования наиболее сильно будут проявляться при малых значе­ниях сигнала и будут весьма малы при больших значениях его (см. рис. 2.10, а нижний график), то, что­бы уменьшить относительные значе­ния искажений квантования, исполь­зуется нелинейное квантование, при котором для малых значений сигна­ла применяют малые, а для больших - большие шаги квантования (рис. 2.10,б). При этом абсолют­ное значение искажений квантования растет (см. средний график), a относительное уменьшается (нижняя часть рисунка).

Изменение напряжения на выходе относительно напряжения на входе устройства, обеспечивающего ука­занную нелинейную зависимость, должно быть таким, как на рис. 2.11. При этом по осям отложены от­носительные величины напряжений на входе х = u_вх/u_вхmах и выходе

У = u_вых/ u_вхmах схемы.

Определим искомую зависимость у = f(x) исходя из условий, вытекаю­щих из графика, приведенного рис. 2.11.

Приращение должно быть обрат­но пропорционально крутизне ха­рактеристики (т. е. производной dy/dx)x = C₁/(dy/dx).

Для обеспечения равенства отно­сительных искажений должно быть выполнено условие х/х = С₂ - по­стоянная величина.

Подставим значение х:

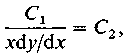
отсюда

Интегрируя         

получим

где In-постоянная интегрирования.

Отсюда

Для нахождения постоянных не обходимо учитывать начальные условия:

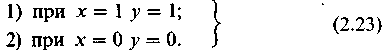
Очевидно, что по условию реше­ние (2.22) нереализуемо. Это опре­деляется тем, что график найден­ной функции будет таким, как на рис. 2.12.

Для получения реализуемого вы­ражения можно использовать два пути.

1. Чтобы выполнить условие 2 введем в выражение (2.22) постоян­ную С₃у = С3 In(х + С₄) и из этого же условия 0 = С₃ In (0 + С₄) нахо­дим С₄ = 1.

Тогда на основании условия  1=С₃1п(+1) определяем С₃ = = 1/1п(+1).

Окончательное решение получим в виде

Это выражение называется лога­рифмической характеристикой ком­прессии типа u.

2. Если считать, что выражение (2.22) будет действительно только на участке от у = 1 до точки k (см. рис. 2.12), в которой касательная к функции у проходит через начало координат (штриховая линия), то на основании выражения (2.22) и усло­вия 1 (2.23) перепишется: 1 = С₃ In , С3 = 1/1 In . Тогда у = In x/ln. Ес­ли принять  = еА, где е основание натуральных логарифмов, то

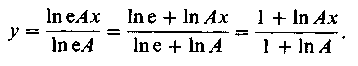
Но по условию эта функция действу­ет только до точки k (см рис. 2. 12), при которой х — а. В этой точке прямая у = Вх (проходящая через начало координат) будет равна зна­чению у при х = а:

Однако в этой же точке равны производные обеих функций, т. е.

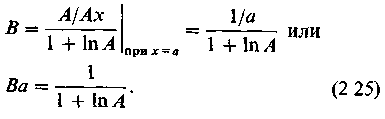
Приравнивая выражения (2.24) и (2.25), получим 1+lnАа=1, что возможно только, если а = 1/А. От­сюда B = А/(1 + In А).